题目内容
已知函数f(x)=sin2x-(
)|x|+
,给出下列结论:
①f(x)是偶函数;
②f(x)的最小值为-
;
③f(x)的最大值为
;
④当x>2015时,f(x)>
恒成立.
其中正确结论的序号是 .(写出所有正确结论的序号)
| 2 |
| 3 |
| 1 |
| 2 |
①f(x)是偶函数;
②f(x)的最小值为-
| 1 |
| 2 |
③f(x)的最大值为
| 3 |
| 2 |
④当x>2015时,f(x)>
| 1 |
| 2 |
其中正确结论的序号是
考点:命题的真假判断与应用
专题:函数的性质及应用
分析:分别根据函数的奇偶性和单调性进行判断即可.
解答:
解:①函数的定义域为为R,
则f(-x)=sin2x-(
)|-x|+
=sin2x-(
)|x|+
=f(x),
则函数f(x)是偶函数;故①正确,
②当x=kπ,k∈Z时,sinx=0,即sin2x的最小值为0,
∵(
)|x|∈(0,1],
∴-(
)|x|∈[-1,0),当且仅当x=0时,取最小值,
∴当x=0时,函数f(x)的最小值为0-1+
=-
;故②正确,
③∵-(
)|x|∈[-1,0),∴-(
)|x|无最大值,
则f(x)的为最大值,故③错误;
④取特殊值当x=1000π时,x>2015,sin21000π=0,且(
)1000π>0
∴f(1000π)=
-(
)1000π<
,因此结论④错.
故答案为:①②
则f(-x)=sin2x-(
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
则函数f(x)是偶函数;故①正确,
②当x=kπ,k∈Z时,sinx=0,即sin2x的最小值为0,
∵(
| 2 |
| 3 |
∴-(
| 2 |
| 3 |
∴当x=0时,函数f(x)的最小值为0-1+
| 1 |
| 2 |
| 1 |
| 2 |
③∵-(
| 2 |
| 3 |
| 2 |
| 3 |
则f(x)的为最大值,故③错误;
④取特殊值当x=1000π时,x>2015,sin21000π=0,且(
| 2 |
| 3 |
∴f(1000π)=
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
故答案为:①②
点评:本题主要考查函数奇偶性的判断及借助不等式知识对函数值域范围进行判断,涉及到函数奇偶性的判断,同时还涉及到三角函数、指数函数的范围问题,利用不等式的放缩求新函数的范围.综合性强

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
函数y=log2x的反函数是( )
| A、y=-log2x |
| B、y=x2 |
| C、y=2x |
| D、y=logx2 |
定义在R上的偶函数f(x)满足:对任意x1,x2∈[1,+∞),且x1≠x2都有
>0,则( )
| f(x1)-f(x2) |
| x1-x2 |
A、f(-
| ||
B、f(2)<f(-
| ||
C、f(2)<f(-1)<f(-
| ||
D、f(-1)<f(-
|
若对数式log(t-2)3有意义,则实数t的取值范围是( )
| A、[2,+∞) |
| B、(2,3)∪(3,+∞) |
| C、(-∞,2) |
| D、(2,+∞) |
在复平面内,复数
,
(i为虚数单位)对应的点分别为A,B,若点C为线段AB的中点,则点C对应的复数为( )
| 1 |
| 1+i |
| 1 |
| 1-i |
A、
| ||
| B、1 | ||
C、
| ||
| D、i |
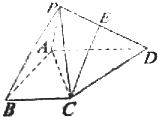 如图所示,四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面所成的角为45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,PA=BC=
如图所示,四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面所成的角为45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,PA=BC=