题目内容
已知一个四边形的四个顶点的坐标分别是A(1,1),B(3,-2),C(-2,-3),D(2,-4),求它的面积.
考点:两点间距离公式的应用,点到直线的距离公式
专题:直线与圆
分析:由题意可得BC的距离和BC的方程,进而可得A、D到BC的距离,由三角形的面积公式可得.
解答:
解:∵四边形的四个顶点的坐标分别是A(1,1),B(3,-2),C(-2,-3),D(2,-4),
∴kBC=
=
,∴BC的方程为y+2=
(x-3),即x-5y-13=0,
∴A到BC的距离d1=
=
,同理可得D到BC的距离d2=
,
再由两点间的距离公式可得|BC|=
=
,
∴原四边形ABDC的面积S=
×
×
+
×
×
=13
∴kBC=
| -3-(-2) |
| -2-3 |
| 1 |
| 5 |
| 1 |
| 5 |
∴A到BC的距离d1=
| |1-5-13| | ||
|
| 17 | ||
|
| 9 | ||
|
再由两点间的距离公式可得|BC|=
| (3+2)2+(-2+3)2 |
| 26 |
∴原四边形ABDC的面积S=
| 1 |
| 2 |
| 26 |
| 17 | ||
|
| 1 |
| 2 |
| 26 |
| 9 | ||
|
点评:本题考查两点间的距离公式和点到直线的距离公式,属基础题.

练习册系列答案
相关题目
已知a>1,e=2.71828…是自然对数的底数,若函数y=logax与y=ax的图象与直线y=x相切于同一点,则a=( )
| A、ee | ||
| B、e2 | ||
| C、e | ||
D、e
|
定义行列式运算:
=a1a4-a2a3.若将函数f(x)=
的图象向左平移m(m>0)个单位后,所得图象对应的函数为奇函数,则m的最小值是( )
|
|
A、
| ||
B、
| ||
C、
| ||
D、
|
若直线ax+2y+1=0与直线x+y-2=0互相垂直,则实数a=( )
| A、1 | ||
| B、-2 | ||
C、-
| ||
D、-
|
定义在R上的偶函数f(x)满足:对任意x1,x2∈[1,+∞),且x1≠x2都有
>0,则( )
| f(x1)-f(x2) |
| x1-x2 |
A、f(-
| ||
B、f(2)<f(-
| ||
C、f(2)<f(-1)<f(-
| ||
D、f(-1)<f(-
|
-i(1-i)2=( )
| A、-2 | B、2 | C、-2i | D、2i |

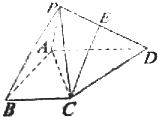 如图所示,四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面所成的角为45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,PA=BC=
如图所示,四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面所成的角为45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,PA=BC=