题目内容
设z的共轭复数是
,且z+
=4,z•
=8,则
等于( )
. |
| z |
. |
| z |
. |
| z |
| ||
| z |
| A、±1 | B、±i | C、1 | D、-i |
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:设z=a+bi(a,b∈R),由于z+
=4,z•
=8,可得2a=4,a2+b2=8,解得a,b.再利用复数的运算法则即可得出.
. |
| z |
. |
| z |
解答:
解:设z=a+bi(a,b∈R),
∵z+
=4,z•
=8,
∴2a=4,a2+b2=8,
解得a=2,b=±2.
∴z=2±2i.
当z=2+2i时,则
=
=
=
=i.
同理当z=2-2i时,则
=-i.
故
=±i.
故选:B.
∵z+
. |
| z |
. |
| z |
∴2a=4,a2+b2=8,
解得a=2,b=±2.
∴z=2±2i.
当z=2+2i时,则
| ||
| z |
| 2-2i |
| 2+2i |
| (1-i)2 |
| (1+i)(1-i) |
| -2i |
| 2 |
同理当z=2-2i时,则
| ||
| z |
故
| ||
| z |
故选:B.
点评:本题考查了复数的运算法则,属于基础题.

练习册系列答案
相关题目
定义行列式运算:
=a1a4-a2a3.若将函数f(x)=
的图象向左平移m(m>0)个单位后,所得图象对应的函数为奇函数,则m的最小值是( )
|
|
A、
| ||
B、
| ||
C、
| ||
D、
|
-i(1-i)2=( )
| A、-2 | B、2 | C、-2i | D、2i |
在复平面内,复数
,
(i为虚数单位)对应的点分别为A,B,若点C为线段AB的中点,则点C对应的复数为( )
| 1 |
| 1+i |
| 1 |
| 1-i |
A、
| ||
| B、1 | ||
C、
| ||
| D、i |
已知函数f(x)=Asin(ωx+φ)( A>0,ω>0,|φ|<
)的部分图象如图所示,则φ=( )
| π |
| 2 |

A、
| ||
B、
| ||
C、-
| ||
D、-
|
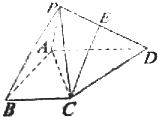 如图所示,四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面所成的角为45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,PA=BC=
如图所示,四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面所成的角为45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,PA=BC=