题目内容
设AB是椭圆的长轴,点C在椭圆上,且∠CBA=
.若AB=4,BC=
,则椭圆的焦距为( )
| π |
| 4 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设椭圆的标准方程为
+
=1,由已知条件推导出2a=4,点C的坐标为C(-1,1),由此能求出c=
,从而能求出椭圆的焦距.
| x2 |
| a2 |
| y2 |
| b2 |
2
| ||
| 3 |
解答:
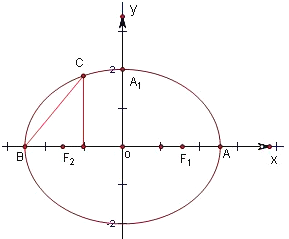 解:如图,设椭圆的标准方程为
解:如图,设椭圆的标准方程为
+
=1,
由题意知,2a=4,a=2.
∵∠CBA=
,BC=
,可设C(y0-2,y0),
∵B(-2,0),
∴
=(y0,y0),
∴|
|=
y0=
,解得y0=1,
∴点C的坐标为C(-1,1),
∵点C在椭圆上,∴
+
=1,
∴b2=
,
∴c2=a2-b2=4-
=
,c=
,
∴椭圆的焦距为
.
故选:C.
 解:如图,设椭圆的标准方程为
解:如图,设椭圆的标准方程为 | x2 |
| a2 |
| y2 |
| b2 |
由题意知,2a=4,a=2.
∵∠CBA=
| π |
| 4 |
| 2 |
∵B(-2,0),
∴
| BC |
∴|
| BC |
| 2 |
| 2 |
∴点C的坐标为C(-1,1),
∵点C在椭圆上,∴
| (-1)2 |
| 4 |
| 12 |
| b2 |
∴b2=
| 4 |
| 3 |
∴c2=a2-b2=4-
| 4 |
| 3 |
| 8 |
| 3 |
2
| ||
| 3 |
∴椭圆的焦距为
4
| ||
| 3 |
故选:C.
点评:本题考查椭圆的焦距的求法,是中档题,解题时要认真审题,注意数形结合思想的合理运用.

练习册系列答案
相关题目
已知△ABC中,a,b,c分别是内角A,B,C所对的边,且3a2+3b2-c2=4ab,则下列结论正确的是( )
| A、sinA≥cosB |
| B、sinA≥sinB |
| C、sinA≤cosB |
| D、cosA≤cosB |
椭圆
+
=1的焦距为2,则m的取值是( )
| x2 |
| m |
| y2 |
| 6 |
| A、7 | B、5 | C、5或7 | D、10 |
函数y=
的定义域是( )
| 4-log2x |
| A、(0,2] |
| B、(0,16] |
| C、(-∞,2] |
| D、(-∞,16] |
已知函数f(n)=
,则f(5)的值是( )
|
| A、4 | B、48 |
| C、240 | D、1440 |
运行如图所示的程序框图,则输出的所有实数对(x,y)所对应的点都在函数( )
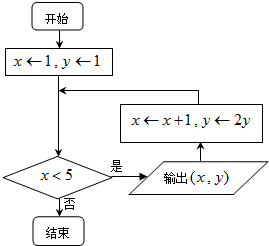

| A、y=x+1的图象上 |
| B、y=2x的图象上 |
| C、y=2x的图象上 |
| D、y=2x-1的图象上 |