题目内容
6．已知f（x）=ex+2xf′（1），则f′（0）等于（ ）| A． | 1+2e | B． | 1-2e | C． | -2e | D． | 2e |
分析 把给出的函数求导得其导函数，在导函数解析式中取x=1可求f′（1）的值，继而求出f′（0）的值．
解答 解：由f（x）=ex+2xf′（1），
得：f′（x）=ex+2f′（1），
取x=1得：f′（1）=e+2f′（1），
所以，f′（1）=-e．
故f′（0）=1-2f′（1）=1-2e，
故答案为：B．
点评 本题考查了导数运算，解答此题的关键是理解原函数解析式中的f′（1），在这里f′（1）只是一个常数，此题是基础题．
练习册系列答案
名校课堂系列答案
相关题目
16．下列幂函数中，定义域是R且又是奇函数的是（ ）
| A． | $y={x^{\frac{3}{2}}}$ | B． | $y={x^{\frac{2}{3}}}$ | C． | $y={x^{-\frac{1}{3}}}$ | D． | $y={x^{\frac{1}{3}}}$ |
1．过点P（-$\sqrt{3}$，-1）的直线l与圆x2+y2=1有公共点，则直线l的倾斜角的取值范围是（ ）
| A． | [0，30°] | B． | [0，45°] | C． | [0，60°] | D． | [0，90°] |
18．在等腰直角△ABC中，过顶点C的直线l与斜边AB相交的概率为（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{3}{4}$ |
15．
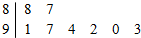某市8所中学生参加比赛的得分用茎叶图表示（如图）其中茎为十位数，叶为个位数，则这组数据的平均数和方差分别是（ ）
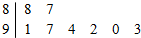某市8所中学生参加比赛的得分用茎叶图表示（如图）其中茎为十位数，叶为个位数，则这组数据的平均数和方差分别是（ ）| A． | 91 5.5 | B． | 91 5 | C． | 92 5.5 | D． | 92 5 |
16．
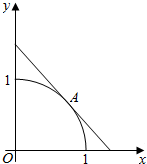如图，设圆弧x2+y2=1（x≥0，y≥0）与两坐标轴正半轴围成的扇形区域为M，过圆弧上中点A做该圆的切线与两坐标轴正半轴围成的三角形区域为N．现随机在区域N内投一点B，若设点B落在区域M内的概率为P，则P的值为（ ）
如图，设圆弧x2+y2=1（x≥0，y≥0）与两坐标轴正半轴围成的扇形区域为M，过圆弧上中点A做该圆的切线与两坐标轴正半轴围成的三角形区域为N．现随机在区域N内投一点B，若设点B落在区域M内的概率为P，则P的值为（ ）| A． | $\frac{π}{4}$ | B． | $\frac{π}{8}$ | C． | $\frac{1}{2}$ | D． | $\frac{1}{4}$ |