题目内容
14．已知椭圆C：$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{8}$=1的右焦点为F2，右准线为l，左焦点为F1，点A∈l，线段AF2交椭圆C于点B，若$\overrightarrow{{F}_{2}A}$=4$\overrightarrow{{F}_{2}B}$，则|BF1|=（ ）| A． | 2 | B． | 4 | C． | 6 | D． | 8 |
分析 由题意可得：点B即为右顶点M，点A（9，0）．即可得出．
解答 解：由椭圆C：$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{8}$=1，可得a=3，c=$\sqrt{9-8}$=1，∴右焦点F2（1，0），右顶点M（3，0），准线l：x=$\frac{{a}^{2}}{c}$=9．
∵$\frac{3-1}{9-1}$=$\frac{1}{4}$，$\overrightarrow{{F}_{2}A}$=4$\overrightarrow{{F}_{2}B}$，
∴点B即为右顶点M，点A（9，0）．
∴|BF1|=a+c=4．
故选：B．
点评 本题考查了椭圆的标准方程及其性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
2．已知PA垂直于△ABC所在的平面，AB=AC=5，BC=6，PA=3，则点A到平面PBC的距离为（ ）
| A． | 4 | B． | $\sqrt{15}$ | C． | $3\sqrt{5}$ | D． | $\frac{12}{5}$ |
9．一椭圆的中心在原点，焦点F1、F2在x轴上，点P是椭圆上一点，线段PF1与y轴的交点M是该线段的中点，若|PF2|=|MF2|，则椭圆的离心率等于（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{\sqrt{3}}{3}$ |
如所示，将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN，使点M，N分别在AB，AD的延长线上，且对角线MN过点C，已知AB=2米，AD=3米．
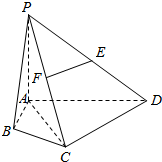如图，在四棱锥P-ABCD中，∠ABC=∠ACD=90°，∠BAC=∠CAD=60°，PA⊥平面ABCD，E为PD的中点，PA=2AB=2
在正棱柱ABCD一A1B1C1D1中，AA1=2AB，若E，F分别为线段A1D1，CC1的中点．求：