题目内容
6.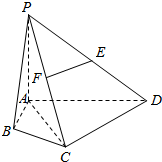 如图,在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2
如图,在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2(1)若F为PC的中点,求证:EF⊥平面PAC;
(2)求四棱锥P-ABCD的体积V.
分析 (1)先证 CD⊥平面PAC,由三角形中位线的性质得EF∥CD,得到EF⊥平面PAC;
(2)把四边形面积分成2个直角三角形面积之和,代入棱锥体积公式进行计算.
解答 (1)证明:∵PA⊥平面ABCD,∴PA⊥CD.
又AC⊥CD,PA∩AC=A,
∴CD⊥平面PAC.
∵E、F分别为PD、PC中点,
∴EF∥CD,
∴EF⊥平面PAC;
(2)解:在Rt△BAC中,∠ABC═90°,∠BAC=60°,AB=1,
∴BC=$\sqrt{3}$,AC=2;
在Rt△DAC中,∠ACD═90°,∠CAD=60°,AC=2,
∴CD=2$\sqrt{3}$,AD=4;
故底面ABCD的面积为S=$\frac{1}{2}$×1×$\sqrt{3}$+$\frac{1}{2}$×2×2$\sqrt{3}$=$\frac{5\sqrt{3}}{2}$
∴VP-ABCD=$\frac{1}{3}$×S×PA=$\frac{1}{3}$×$\frac{5\sqrt{3}}{2}$×2=$\frac{5\sqrt{3}}{3}$.
点评 本题考查用分割法求出棱锥的底面积,直线与平面垂直的判定,考查了学生的空间想象力及计算能力,属于中档题.

练习册系列答案
相关题目
15.已知三棱锥D-ABC的四个顶点均在半径为R的球面上,且AB=BC=$\sqrt{3}$,AC=3,若该三棱锥体积的最大值为$\frac{3\sqrt{3}}{4}$,则R=( )
| A. | 1 | B. | 2 | C. | 3 | D. | $\frac{2}{3}$ |
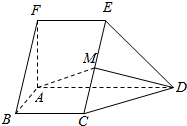 如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,AF=AB=BC=FE=$\frac{1}{2}$AD.
如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,AF=AB=BC=FE=$\frac{1}{2}$AD.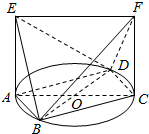 如图,已知AC,BD为圆O的任意两条直径,直线AE,CF是圆O所在平面的两条垂线,且线段AE=CF=$\sqrt{2}$,AC=2.
如图,已知AC,BD为圆O的任意两条直径,直线AE,CF是圆O所在平面的两条垂线,且线段AE=CF=$\sqrt{2}$,AC=2.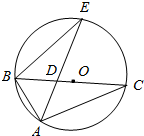 如图,△ABC内接于圆O,AE平分∠BAC交BC于点D,连接BE.
如图,△ABC内接于圆O,AE平分∠BAC交BC于点D,连接BE.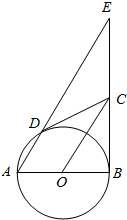 如图,AB为圆O的直径,CB是圆O的切线,弦AD∥OC.
如图,AB为圆O的直径,CB是圆O的切线,弦AD∥OC.