题目内容
14.若一个底面边长为$\frac{\sqrt{6}}{2}$,侧棱长为$\sqrt{6}$的正六棱柱的所有顶点都在一个球面上,求该球的体积和表面积.分析 正六棱柱的体对角线就是外接球的直径,求出即可求其体积和表面积.
解答 解:根据条件正六棱柱的最长的对角线为球的直径,
由(2R)2=6+6得R=$\sqrt{3}$,球体积为$\frac{4}{3}•π•(\sqrt{3})^{3}$=4$\sqrt{3}π$,
表面积$4π•(\sqrt{3})^{2}$=12π.
点评 本题考查球的体积和表面积,棱柱的体对角线问题,考查空间想象能力,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.下列函数中,是奇函数的是( )
| A. | y=-|x| | B. | y=$\frac{1}{x}$ | C. | y=3-x | D. | y=2x |
13.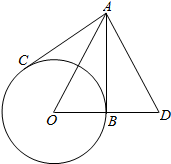 如图,AB,AC为⊙O的切线,B和C是切点,延长OB到D,使BD=OB,连接AD.如果∠DAC=78°,那么∠ADO等于( )
如图,AB,AC为⊙O的切线,B和C是切点,延长OB到D,使BD=OB,连接AD.如果∠DAC=78°,那么∠ADO等于( )
 如图,AB,AC为⊙O的切线,B和C是切点,延长OB到D,使BD=OB,连接AD.如果∠DAC=78°,那么∠ADO等于( )
如图,AB,AC为⊙O的切线,B和C是切点,延长OB到D,使BD=OB,连接AD.如果∠DAC=78°,那么∠ADO等于( )| A. | 70° | B. | 64° | C. | 62° | D. | 51° |