题目内容
2.已知PA垂直于△ABC所在的平面,AB=AC=5,BC=6,PA=3,则点A到平面PBC的距离为( )| A. | 4 | B. | $\sqrt{15}$ | C. | $3\sqrt{5}$ | D. | $\frac{12}{5}$ |
分析 利用等体积法,求解点A到平面PBC的距离.
解答 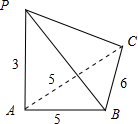 解:PA垂直于△ABC所在的平面,AB=AC=5,BC=6,PA=3,
解:PA垂直于△ABC所在的平面,AB=AC=5,BC=6,PA=3,
可得PB=PC=$\sqrt{9+25}$=$\sqrt{34}$.
底面三角形ABC的面积为:$\frac{1}{2}×6×\sqrt{{5}^{2}-{3}^{2}}$=12,
棱锥是体积为:$\frac{1}{3}×12×3$=12.
点A到平面PBC的距离为h.
VA-PBC=$\frac{1}{3}×{S}_{△PBC}•h$=$\frac{1}{3}×\frac{1}{2}×6×\sqrt{34-{3}^{2}}$•h=5h,
可得:5h=12,
h=$\frac{12}{5}$,
故选:D.
点评 本题考查点到平面的距离距离公式的求法,考查计算能力.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
2.下列函数中,是奇函数的是( )
| A. | y=-|x| | B. | y=$\frac{1}{x}$ | C. | y=3-x | D. | y=2x |
13.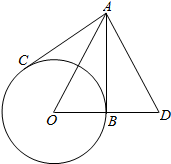 如图,AB,AC为⊙O的切线,B和C是切点,延长OB到D,使BD=OB,连接AD.如果∠DAC=78°,那么∠ADO等于( )
如图,AB,AC为⊙O的切线,B和C是切点,延长OB到D,使BD=OB,连接AD.如果∠DAC=78°,那么∠ADO等于( )
 如图,AB,AC为⊙O的切线,B和C是切点,延长OB到D,使BD=OB,连接AD.如果∠DAC=78°,那么∠ADO等于( )
如图,AB,AC为⊙O的切线,B和C是切点,延长OB到D,使BD=OB,连接AD.如果∠DAC=78°,那么∠ADO等于( )| A. | 70° | B. | 64° | C. | 62° | D. | 51° |
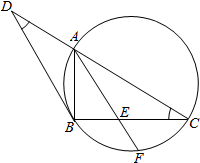 如图,BD是△ABC外接圆的切线,过A作BD的平行线交BC于E,交△ABC的外接圆于F.
如图,BD是△ABC外接圆的切线,过A作BD的平行线交BC于E,交△ABC的外接圆于F.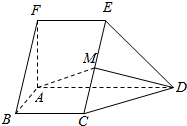 如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,AF=AB=BC=FE=$\frac{1}{2}$AD.
如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,AF=AB=BC=FE=$\frac{1}{2}$AD.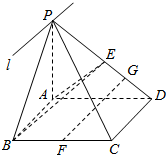 如图,四棱锥P-ABCD,底面ABCD为平行四边形,E、F分别为 PD、BC的中点,面PAB∩面PCD=l.
如图,四棱锥P-ABCD,底面ABCD为平行四边形,E、F分别为 PD、BC的中点,面PAB∩面PCD=l.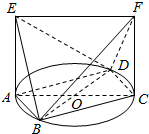 如图,已知AC,BD为圆O的任意两条直径,直线AE,CF是圆O所在平面的两条垂线,且线段AE=CF=$\sqrt{2}$,AC=2.
如图,已知AC,BD为圆O的任意两条直径,直线AE,CF是圆O所在平面的两条垂线,且线段AE=CF=$\sqrt{2}$,AC=2.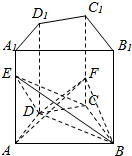 如图,在直四棱柱ABCD-A1B1C1D1中,点E,F分别在AA1,CC1上,且AE=$\frac{4}{5}$AA1,CF=$\frac{1}{3}$CC1,点A,C到BD的距离之比为2:3,则三棱锥E-BCD和F-ABD的体积比$\frac{{V}_{E-BCD}}{{V}_{F-ABD}}$=$\frac{18}{5}$.
如图,在直四棱柱ABCD-A1B1C1D1中,点E,F分别在AA1,CC1上,且AE=$\frac{4}{5}$AA1,CF=$\frac{1}{3}$CC1,点A,C到BD的距离之比为2:3,则三棱锥E-BCD和F-ABD的体积比$\frac{{V}_{E-BCD}}{{V}_{F-ABD}}$=$\frac{18}{5}$.