题目内容
5.已知抛物线y2=2px的准线与x2-y2=2的左准线重合,则抛物线的焦点为(1,0).分析 先整理双曲线方程为标准方程,进而求得c,则双曲线准线方程可得,进而求得抛物线方程中的p,则抛物线的焦点坐标可得.
解答 解:整理双曲线方程得$\frac{{x}^{2}}{2}-\frac{{y}^{2}}{2}$=1,
∴a=$\sqrt{2}$,b=$\sqrt{2}$,c=2,
∴双曲线的左准线方程为x=-$\frac{{a}^{2}}{c}$=-1
∴抛物线的准线方程为x=-1,
∴p=2,
∴抛物线的焦点坐标为(1,0),
故答案为:(1,0).
点评 本题主要考查了抛物线的简单性质,圆锥曲线的共同特征.考查了学生对基础知识的综合把握能力.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
13.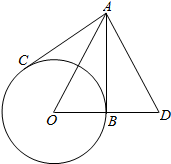 如图,AB,AC为⊙O的切线,B和C是切点,延长OB到D,使BD=OB,连接AD.如果∠DAC=78°,那么∠ADO等于( )
如图,AB,AC为⊙O的切线,B和C是切点,延长OB到D,使BD=OB,连接AD.如果∠DAC=78°,那么∠ADO等于( )
 如图,AB,AC为⊙O的切线,B和C是切点,延长OB到D,使BD=OB,连接AD.如果∠DAC=78°,那么∠ADO等于( )
如图,AB,AC为⊙O的切线,B和C是切点,延长OB到D,使BD=OB,连接AD.如果∠DAC=78°,那么∠ADO等于( )| A. | 70° | B. | 64° | C. | 62° | D. | 51° |
15.已知三棱锥D-ABC的四个顶点均在半径为R的球面上,且AB=BC=$\sqrt{3}$,AC=3,若该三棱锥体积的最大值为$\frac{3\sqrt{3}}{4}$,则R=( )
| A. | 1 | B. | 2 | C. | 3 | D. | $\frac{2}{3}$ |
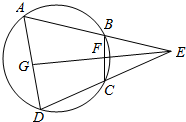 如图,已知四边形ABCD内接于圆,延长AB和DC交于E,EG平分∠E,且与BC、AD别相交于F、G.求证:∠CFG=∠DGF.
如图,已知四边形ABCD内接于圆,延长AB和DC交于E,EG平分∠E,且与BC、AD别相交于F、G.求证:∠CFG=∠DGF.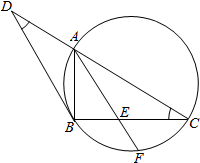 如图,BD是△ABC外接圆的切线,过A作BD的平行线交BC于E,交△ABC的外接圆于F.
如图,BD是△ABC外接圆的切线,过A作BD的平行线交BC于E,交△ABC的外接圆于F.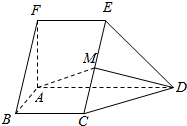 如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,AF=AB=BC=FE=$\frac{1}{2}$AD.
如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,AF=AB=BC=FE=$\frac{1}{2}$AD.