题目内容
14.解不等式组:$\left\{\begin{array}{l}{\frac{x-3}{x}≥2}\\{|4x+5|>3}\end{array}\right.$.分析 分别解分式不等式和绝对值不等式,取交集可得.
解答 解:不等式$\frac{x-3}{x}$≥2可化为$\frac{x-3}{x}$-2≥0,
通分并整理可得$\frac{x+3}{x}$≤0,解得-3≤x<0;
不等式|4x+5|>3可化为4x+5<-3或4x+5>3,
解得x<-2或x>-$\frac{1}{2}$,
取交集可得原不等式的解集为{x|-3≤x<-2或-$\frac{1}{2}$<x<0}
点评 本题考查不等式组的解集,涉及分式不等式和绝对值不等式,属基础题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
4.若3a+4b=ab,a>0且b>0,则a+b的最小值是( )
| A. | $6+2\sqrt{3}$ | B. | $7+2\sqrt{3}$ | C. | $6+4\sqrt{3}$ | D. | $7+4\sqrt{3}$ |
5.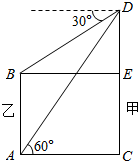 如图,甲、乙两楼相距20米,从乙楼底望甲楼顶的仰角为60°,从甲楼顶望乙楼顶的俯角为30°,则乙楼的高是( )
如图,甲、乙两楼相距20米,从乙楼底望甲楼顶的仰角为60°,从甲楼顶望乙楼顶的俯角为30°,则乙楼的高是( )
 如图,甲、乙两楼相距20米,从乙楼底望甲楼顶的仰角为60°,从甲楼顶望乙楼顶的俯角为30°,则乙楼的高是( )
如图,甲、乙两楼相距20米,从乙楼底望甲楼顶的仰角为60°,从甲楼顶望乙楼顶的俯角为30°,则乙楼的高是( )| A. | $\frac{40\sqrt{3}}{3}$ | B. | 20$\sqrt{3}$ | C. | 40 | D. | 10$\sqrt{2}$ |
9.“x<4”是“$\sqrt{x}$<2”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
6.设a∈Z,且0≤a<13,若512015+a能被13整除,则a=( )
| A. | 0 | B. | 1 | C. | 11 | D. | 12 |