Question

5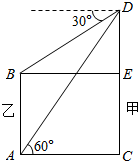．如图，甲、乙两楼相距20米，从乙楼底望甲楼顶的仰角为60°，从甲楼顶望乙楼顶的俯角为30°，则乙楼的高是（　　）

• A． $\frac{40\sqrt{3}}{3}$
• B． 20$\sqrt{3}$
• C． 40
• D． 10$\sqrt{2}$

Answer 1

分析 设甲、乙两楼的位置分别为CD、AB如图所示．直角三角形ABD中利用三角函数的定义，结合题中数据算出BD=$\frac{40\sqrt{3}}{3}$m，再在△ABD中，算出∠BAD=∠BDA=30°，从而得到AB=BD=$\frac{40\sqrt{3}}{3}$m，由此得到乙楼的高．

解答 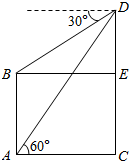解：设甲、乙两楼的位置分别为CD、AB如图所示
∵Rt△BDE中，BE=AC=20m，∠BDE=60°
∴BD=$\frac{BE}{sin60°}$=$\frac{40\sqrt{3}}{3}$m
又∵△ABD中，∠BAD=∠BDA=30°
∴△ABD为等腰三角形，得AB=BD=$\frac{40\sqrt{3}}{3}$m
即乙楼的高$\frac{40\sqrt{3}}{3}$m
故选：A．

点评 本题给出两幢楼的距离，在已知楼底望楼顶的仰角和楼顶望楼顶的俯角情况下，求乙楼的高度．着重考查了直角三角形中三角函数的定义和解三角形的实际应用等知识，属于基础题．