题目内容
如图,在四边形ABCD中,已AB=1,BC=2,CD=3,∠ABC=120°,∠BCD=90°,则边AD的长为 .


考点:解三角形的实际应用
专题:综合题,解三角形
分析:如图,过点A作AM垂直BC于M,过点A作AN垂直CD于N,在直角三角形AND中,由勾股定理得AD.
解答:
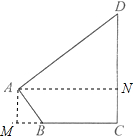 解:如图,过点A作AM垂直BC于M,过点A作AN垂直CD于N,
解:如图,过点A作AM垂直BC于M,过点A作AN垂直CD于N,
因为∠ABC=120°,所以∠ABM=60°,∠BAM=30°,
又因为AB=1,所以BM=
,AM=
,
因为∠BCD=90°,∠ANC=∠AMC=90°,
所以四边形AMCN为矩形,所以CN=AM=
,
又因为CD=3,所以DN=CD-CN=3-
,
又因为AN=MC=MB+BC=
,
在直角三角形AND中,由勾股定理得AD=
故答案为:
.
 解:如图,过点A作AM垂直BC于M,过点A作AN垂直CD于N,
解:如图,过点A作AM垂直BC于M,过点A作AN垂直CD于N,因为∠ABC=120°,所以∠ABM=60°,∠BAM=30°,
又因为AB=1,所以BM=
| 1 |
| 2 |
| ||
| 2 |
因为∠BCD=90°,∠ANC=∠AMC=90°,
所以四边形AMCN为矩形,所以CN=AM=
| ||
| 2 |
又因为CD=3,所以DN=CD-CN=3-
| ||
| 2 |
又因为AN=MC=MB+BC=
| 5 |
| 2 |
在直角三角形AND中,由勾股定理得AD=
16-3
|
故答案为:
16-3
|
点评:本题考查解三角形的实际应用,正确构造直角三角形是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知(3x-1)8=a8x8+a7x7+a6x6+…+a1x1+a0,则 a6+a4+a2+a0的值是( )
| A、27+215-38 |
| B、27+215 |
| C、28-38 |
| D、28+216-1 |