题目内容
已知(3x-1)8=a8x8+a7x7+a6x6+…+a1x1+a0,则 a6+a4+a2+a0的值是( )
| A、27+215-38 |
| B、27+215 |
| C、28-38 |
| D、28+216-1 |
考点:二项式定理的应用
专题:二项式定理
分析:由通项公式求得a8=38,在所给的等式中,分别令x=1、x=-1,可得2个等式,由这两个等式求得a8+a6+a4+a2+a0 的值,可得 a6+a4+a2+a0的值.
解答:
解:二项式(3x-1)8的展开式的通项公式为 Tr+1=
•38-r•(-1)r•x8-r,可得x8的系数为a8=38.
在(3x-1)8=a8x8+a7x7+a6x6+…+a1x1+a0 中,令x=1,可得a0+a1+a2+a3+…+a8=28 ①,
再令x=-1可得得a0-a1+a2-a3+…+a8=48 ②.
由①②求得a8+a6+a4+a2+a0 =27+215,∴a6+a4+a2+a0=27+215-38,
故选:A.
| C | r 8 |
在(3x-1)8=a8x8+a7x7+a6x6+…+a1x1+a0 中,令x=1,可得a0+a1+a2+a3+…+a8=28 ①,
再令x=-1可得得a0-a1+a2-a3+…+a8=48 ②.
由①②求得a8+a6+a4+a2+a0 =27+215,∴a6+a4+a2+a0=27+215-38,
故选:A.
点评:本题主要考查二项式定理的应用,注意根据题意,分析所给代数式的特点,通过给二项式的x赋值,求展开式的系数和,可以简便的求出答案,属于基础题.

练习册系列答案
相关题目
已知O是△ABC的重心,且35a
+21b
+15c
=
,则C=( )
| OA |
| OB |
| OC |
| 0 |
| A、30° | B、60° |
| C、90° | D、120° |
下列各式中,最小值等于2的是( )
| A、logab+logba | ||||
B、
| ||||
C、tanθ+
| ||||
| D、2x+2-x |
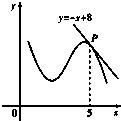 如图,函数y=f(x)的图象在点P处的切线方程是y=-x+8,则f(5)+f′(5)=( )
如图,函数y=f(x)的图象在点P处的切线方程是y=-x+8,则f(5)+f′(5)=( )A、
| ||
| B、1 | ||
| C、2 | ||
| D、0 |
函数y=2cos2(x-
)-1是( )
| π |
| 4 |
| A、最小正周期为π的奇函数 |
| B、最小正周期为2π的奇函数 |
| C、最小正周期为π的偶函数 |
| D、最小正周期为2π的偶函数 |
已知两条不同的直线l,m和两个不同的平面α,β,则下列命题中:①若l∥m,m?α,则l∥α,②若l∥α,m?α,则l∥m,③若l∥α,l∥β,则α∥β,④若α∥β,l∥α,则l∥β,正确命题个数是( )
| A、0 | B、1 | C、2 | D、3 |
i是虚数单位,则1+i+i2+i3=( )
| A、1 | B、i | C、1-i | D、0 |
