题目内容

4．一个几何体的三视图如图所示，则该几何体的表面积是（　　）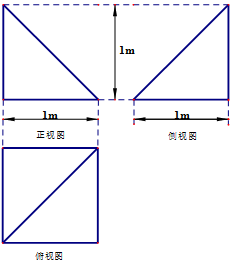
A．$（1+\sqrt{2}）{m^2}$B．$（1+2\sqrt{2}）{m^2}$C．$（2+\sqrt{2}）{m^2}$D．$（2+2\sqrt{2}）{m^2}$

分析 由已知中的三视图可得该几何体是一个以俯视图为底面的四棱锥，求出各个面的面积，相加可得答案．

解答 解：由已知中的三视图可得该几何体是一个以俯视图为底面的四棱锥，
其底面是边长为1m的正方形，故底面积为1m2，
侧面均为直角三角形，
其中有两个是腰为1m的等腰直角三角形，面积均为：$\frac{1}{2}$m2，
另外两个是边长分别为1m，$\sqrt{2}$m，$\sqrt{3}$m的直角三角形，面积均为：$\frac{\sqrt{2}}{2}$m2，
故几何体的表面积S=$（2+\sqrt{2}）{m^2}$，
故选：C

点评 本题考查的知识点是棱锥的表面积和体积，简单几何体的三视图，难度中档．

练习册系列答案
相关题目
14．在数列{an}中，a1=1，a2=2，且an+1=（1+q）an-qan-1（n≥2，q≠0）
（Ⅰ）设bn=an+1-an（n∈N*），证明{bn}是等比数列；
（Ⅱ）当q=2时，求数列{an}的通项公式．
15．如图，四棱锥P-ABCD中，AD∥BC，AD⊥DC，AD=2BC=2CD=2，侧面APD为等腰直角三角形，∠APD=90°，平面PAD⊥平面ABCD，E为棱PC上的一点．
（1）求证：PA⊥DE；
（2）在棱PC上是否存在一点E，使得二面角E-BD-A的余弦值为-$\frac{{\sqrt{3}}}{3}$，若存在，请求出$\frac{EC}{PC}$的值；若不存在，请说明理由．
12．对于二次函数y=-4x2+8x-5，
（1）指出图象的开口方向、对称轴方程、顶点坐标；
（2）画出它的图象，并说明其图象由y=-4x2的图象经过怎样平移得来；
（3）分析函数的单调性．
（4）求函数的最大值或最小值．
19．双曲线与椭圆有共同的焦点F1（-5，0），F2（5，0），点P（4，3）是双曲线的渐近线与椭圆的一个交点，求双曲线与椭圆的方程．
9．已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$过点$A（1，\frac{{2\sqrt{3}}}{3}）$，离心率为$\frac{{\sqrt{3}}}{3}$，左焦点为F．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）若直线l：$x+\sqrt{2}y-1=0$交椭圆于A，B两点，求△FAB的面积．
16．已知双曲线$\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{4}$=1，则其渐近线方程为（　　）
A．y=±$\frac{\sqrt{3}}{3}$xB．y=±$\sqrt{3}$xC．y=±$\frac{1}{3}$xD．y=±3x
13．已知正六棱柱的12个顶点都在一个半径为3的球面上，当正六棱柱的体积最大时，其高的值为（　　）
A．3$\sqrt{3}$B．$\sqrt{3}$C．2$\sqrt{6}$D．2$\sqrt{3}$
14．已知抛物线y2=2px（p＞0），过点K（-4，0）作抛物线的两条切线KA，KB，A，B为切点，若AB过抛物线的焦点，△KAB的面积为24，则p的值是（　　）
A．12B．-12C．8D．4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网