题目内容
在极坐标系中,点P(2,
)到极轴的距离为 .
| π |
| 3 |
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:本题可以利用公式求出点的平面直角坐标,从而得到它在平面直角坐标系中与x轴的距离,即得到点P(2,
)到极轴的距离.
| π |
| 3 |
解答:
解:∵在极坐标系中,点P(2,
),
∴ρ=2,θ=
.
将极点与平面直角坐标系的原点重合,极轴与x轴重合,正方向一致,建立平面直角坐标系,
设P(x,y),
则x=ρcosθ=2cos
=1,
y=ρsinθ=2sin
=
.
∴它在平面直角坐标系中与x轴的距离为:
.
∴到点P(2,
)到极轴的距离为:
.
故答案为:
.
| π |
| 3 |
∴ρ=2,θ=
| π |
| 3 |
将极点与平面直角坐标系的原点重合,极轴与x轴重合,正方向一致,建立平面直角坐标系,
设P(x,y),
则x=ρcosθ=2cos
| π |
| 3 |
y=ρsinθ=2sin
| π |
| 3 |
| 3 |
∴它在平面直角坐标系中与x轴的距离为:
| 3 |
∴到点P(2,
| π |
| 3 |
| 3 |
故答案为:
| 3 |
点评:本题考查了极坐标化成平面直角坐标,本题难度不大,属于基础题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目
由无理数引发的数学危机一直延续到19世纪.直到1872年,德国数学家戴德金从连续性的要求出发,用有理数的“分割”来定义无理数(史称戴德金分割),并把实数理论建立在严格的科学基础上,才结束了无理数被认为“无理”的时代,也结束了持续2000多年的数学史上的第一次大危机.所谓戴德金分割,是指将有理数集Q划分为两个非空的子集M与N,且满足M∪N=Q,M∩N=∅,M中的每一个元素都小于N中的每一个元素,则称(M,N)为戴德金分割试判断,对于任一戴德金分割(M,N),下列选项中,不可能成 立的是( )
| A、M没有最大元素,N有一个最小元素 |
| B、M没有最大元素,N也没有最小元素 |
| C、M有一个最大元素,N有一个最小元素 |
| D、M有一个最大元素,N没有最小元素 |
已知非空数集A、B、C,若A={y|y=x2,x∈B},B={y|y=
,x∈C},C={y|y=x3,x∈A},则( )
| x |
| A、A=B=C |
| B、A=B≠C |
| C、A=C≠B |
| D、B=C≠A |
已知A,B,C,D为四个不同点,且
+
+
+
=
,则( )
| AB |
| BC |
| CD |
| DA |
| 0 |
| A、A,B,C,D四点必共面 |
| B、A,B,C,D四点构成一个空间四边形 |
| C、A,B,C,D四点必共线 |
| D、A,B,C,D四点的位置无法确定 |
某同学设计如图所示的程序框图用以计算和式12+22+32+…+202的值,则在判断框中应填写( )


| A、i≤9 | B、i≥9 |
| C、i≤20 | D、i≥11 |
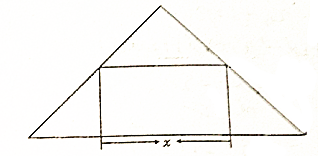 有一块直角边为
有一块直角边为