题目内容
16. 如图,直三棱柱ABC-A1B1C1中,底面ABC为等腰直角三角形,AB⊥AC,AB=AC=2,AA1=3,M是侧棱CC1上一点.
如图,直三棱柱ABC-A1B1C1中,底面ABC为等腰直角三角形,AB⊥AC,AB=AC=2,AA1=3,M是侧棱CC1上一点.(1)若BM⊥A1C,求$\frac{{{C_1}M}}{MC}$的值;
(2)若MC=2,求直线BA1与平面ABM所成角的正弦值.
分析 (1)以A为坐标原点,以射线AB、AC、AA1分别为x、y、z轴建立空间直角坐标系,求出相关点的坐标,$\overrightarrow{BM}=({-2,2,h})$,$\overrightarrow{{A_1}C}=({0,2,-3})$,由BM⊥A1C得$\overrightarrow{BM}•\overrightarrow{{A_1}C}=0$,求出h,然后推出$\frac{{{C_1}M}}{MC}$的值.
(2)求出平面ABM的一个法向量,利用空间向量数量积求解直线BA1与平面ABM所成的角为θ的余弦函数值,即可求解直线BA1与平面ABM所成的角正弦值.
解答 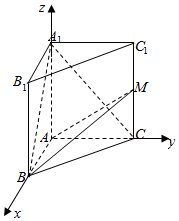 解:(1)以A为坐标原点,以射线AB、AC、AA1
解:(1)以A为坐标原点,以射线AB、AC、AA1
分别为x、y、z轴建立空间直角坐标系,…(1分)
如图所示,则B(2,0,0),A1(0,0,3),C(0,2,0),
设MC=h,则 M(0,2,h)$\overrightarrow{BM}=({-2,2,h})$,$\overrightarrow{{A_1}C}=({0,2,-3})$…(2分)
由BM⊥A1C得$\overrightarrow{BM}•\overrightarrow{{A_1}C}=0$,即2×2-3h=0
解得$h=\frac{4}{3}$,…(5分)
故$\frac{{{C_1}M}}{MC}=\frac{5}{4}$; …(7分)
(2)因为MC=2,所以M(0,2,2),$\overrightarrow{AB}=({2,0,0}),\overrightarrow{AM}=({0,2,2}),\overrightarrow{B{A_1}}=({-2,0,3})$
设平面ABM的一个法向量为$\vec n=({x,y,z})$,由$\left\{\begin{array}{l}{\vec n•\overrightarrow{AB}=0}\\{\vec n•\overrightarrow{AM}=0}\end{array}$得$\left\{\begin{array}{l}{x=0}\\{y+z=0}\end{array}$,
所以$\vec n=({0,1,-1})$,…(10分)
则cos$<\overrightarrow{n},\overrightarrow{B{A}_{1}}>$=$\frac{\overrightarrow{n}•\overrightarrow{B{A}_{1}}}{|\overrightarrow{n}||\overrightarrow{B{A}_{1}}|}$=$\frac{-3}{\sqrt{2}•\sqrt{13}}$=-$\frac{3\sqrt{26}}{26}$,…(14分)
设直线BA1与平面ABM所成的角为θ,所以sinθ=|cos$<\overrightarrow{n},\overrightarrow{B{A}_{1}}>$|=$\frac{3\sqrt{26}}{26}$,
所以直线BA1与平面ABM所成的角正弦值为$\frac{{3\sqrt{26}}}{26}$.…(16分).
点评 本题考查空间向量的数量积的应用,空间向量的垂直,以及线面角的求法,考查空间想象能力以及计算能力.

 通城学典默写能手系列答案
通城学典默写能手系列答案 如图,在△ABC中,D是边BC上一点,$\overrightarrow{BD}=2\overrightarrow{DC},|{\overrightarrow{AD}}$|=1.
如图,在△ABC中,D是边BC上一点,$\overrightarrow{BD}=2\overrightarrow{DC},|{\overrightarrow{AD}}$|=1.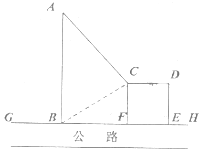 如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建设一仓库,设AB=ykm,并在公路北侧建造边长为xkm的正方形无顶中转站CDEF(其中EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且∠ABC=60°..
如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建设一仓库,设AB=ykm,并在公路北侧建造边长为xkm的正方形无顶中转站CDEF(其中EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且∠ABC=60°..