题目内容
5.已知函数f(x)=$\left\{\begin{array}{l}{\frac{1}{x+1}-3,-1<x≤0}\\{x,0<x≤1}\end{array}\right.$,若函数g(x)=f(x)-mx-m在(-1,1]内有且仅有两个不同的零点,则实数m的取值范围为($-\frac{9}{4}$,-2]∪(0,$\frac{1}{2}$].分析 由g(x)=f(x)-mx-m=0,即f(x)=m(x+1),作出两个函数的图象,利用数形结合即可得到结论.
解答 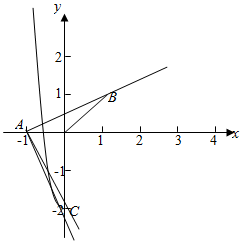 解:由g(x)=f(x)-mx-m=0,即f(x)=m(x+1),
解:由g(x)=f(x)-mx-m=0,即f(x)=m(x+1),
分别作出函数f(x)和y=h(x)=m(x+1)的图象如图:
由图象可知f(1)=1,h(x)表示过定点A(-1,0)的直线,
当h(x)过(1,1)时,m=$\frac{1}{2}$,此时两个函数有两个交点,
此时满足条件的m的取值范围是0<m≤$\frac{1}{2}$,
当h(x)过(0,-2)时,h(0)=-2,解得m=-2,此时两个函数有两个交点,
当h(x)与f(x)相切时,两个函数只有一个交点,此时 $\frac{1}{x+3}$x-3=m(x+1)即m(x+1)2+3(x+1)-1=0,
当m=0时,只有1解,当m≠0,由△=9+4m=0得m=-$\frac{9}{4}$,此时直线和f(x)相切,
∴要使函数有两个零点,则-$\frac{9}{4}$<m≤-2或0<m≤$\frac{1}{2}$.
故答案为:($-\frac{9}{4}$,-2]∪(0,$\frac{1}{2}$].
点评 本题主要考查函数零点的应用,利用数形结合是解决此类问题的基本方法,属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
14.若X是离散型随机变量,P(X=x1)=$\frac{2}{3}$,P(X=x2)=$\frac{1}{3}$,且x1<x2,又已知E(X)=$\frac{4}{3}$,D(X)=$\frac{2}{9}$,则x1+x2的值为( )
| A. | $\frac{5}{3}$ | B. | $\frac{7}{3}$ | C. | 3 | D. | $\frac{11}{3}$ |
14.若函数f(x)=mlnx+x2-mx在区间(0,+∞)内单调递增.则实数m的取值范围为( )
| A. | [0,8] | B. | (0,8] | C. | (-∞,0]∪[8,+∞) | D. | (-∞,0)∪(8,+∞) |
 如图,直三棱柱ABC-A1B1C1中,底面ABC为等腰直角三角形,AB⊥AC,AB=AC=2,AA1=3,M是侧棱CC1上一点.
如图,直三棱柱ABC-A1B1C1中,底面ABC为等腰直角三角形,AB⊥AC,AB=AC=2,AA1=3,M是侧棱CC1上一点.