题目内容
正方体ABCD-A1B1C1D1中，棱长为a，M、N分别是AB1、A1C1上的点，A1N=AM，
（1）求证：MN∥BB1C1C；
（2）求MN的长度最小值．
（1）求证：MN∥BB1C1C；
（2）求MN的长度最小值．
考点：直线与平面平行的判定,直线与平面所成的角
专题：综合题,空间位置关系与距离
分析：（1）作NE∥A1B1交B1C1于E，作MF∥AB交BB1于F，连结EF，证明四边形MNEF是平行四边形，利用线面平行的判定定理证明MN∥BB1C1C；
（2）设B1E=x，求出B1F，利用勾股定理，结合配方法，即可求MN的长度最小值．
（2）设B1E=x，求出B1F，利用勾股定理，结合配方法，即可求MN的长度最小值．
解答：
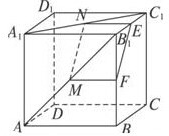（1）证明：作NE∥A1B1交B1C1于E，作MF∥AB交BB1于F，连结EF，则NE∥MF．
∵NE∥A1B1，
∴
=
．
又MF∥AB∥A1B1，∴
=
．
∵A1C1=AB1，A1N=AM，
∴C1N=B1M．∴
=
．
又AB=A1B1，∴NE=MF．
∴四边形MNEF是平行四边形，
∴MN∥EF，且MN=EF．
又MN?平面BB1C1C，EF?平面BB1C1C，
∴MN∥平面BB1C1C．
（2）解：设B1E=x．
∵NE∥A1B1，∴
=
．
又∵MF∥AB，∴
=
．
∵A1N=AM，A1C1=AB1=
a，B1C1=BB1=a，B1E=x，
∴
+
=1．∴B1F=a-x．
从而MN=EF=
=
．
∴当x=
时，MN取得最小值为
a．
（1）证明：作NE∥A1B1交B1C1于E，作MF∥AB交BB1于F，连结EF，则NE∥MF．∵NE∥A1B1，
∴
| NE |
| A1B1 |
| C1N |
| A1C1 |
又MF∥AB∥A1B1，∴
| MF |
| AB |
| B1M |
| AB1 |
∵A1C1=AB1，A1N=AM，
∴C1N=B1M．∴
| NE |
| A1B1 |
| MF |
| AB |
又AB=A1B1，∴NE=MF．
∴四边形MNEF是平行四边形，
∴MN∥EF，且MN=EF．
又MN?平面BB1C1C，EF?平面BB1C1C，
∴MN∥平面BB1C1C．
（2）解：设B1E=x．
∵NE∥A1B1，∴
| B1E |
| B1C1 |
| A1N |
| A1C1 |
又∵MF∥AB，∴
| B1F |
| BB1 |
| B1M |
| AB1 |
∵A1N=AM，A1C1=AB1=
| 2 |
∴
| x |
| a |
| B1F |
| a |
从而MN=EF=
| x2+(a-x)2 |
2(x-
|
∴当x=
| a |
| 2 |
| ||
| 2 |
点评：本题考查线面平行的判定定理，考查MN的长度最小值，考查学生的计算能力，考查学生分析解决问题的能力，正确运用线面平行的判定定理是关键．
练习册系列答案
53随堂测系列答案
相关题目
已知集合A={-2，0，2}，B={x|x2-x-2=0}，则A∩B=（ ）
| A、∅ |
| B、{ 2} |
| C、{ 0} |
| D、{-2} |
若动点M（x，y）到点F（4，0）的距离等于它到直线x+4=0距离，则M点的轨迹方程是（ ）
| A、x+4=0 |
| B、x-4=0 |
| C、y2=8x |
| D、y2=16x |
