题目内容
某旅游景点为了增加人气,吸引游客,特推出一系列活动.其中有一项活动是:凡购买该景点门票的游客,可参加一次抽奖:掷两枚6个面分别标有数字1,2,3,4,5,6的正方体骰子,点数之和为12点获一等奖,奖品价值120元;点数之和为11点或10点获二等奖,奖品价值60元;点数之和为9点或8点获三等奖,奖品价值20元;点数之和小于8点的不得奖.
(1)求同行的两位游客中一人获一等奖、一人获二等奖的概率;
(2)设一位游客在该景点处获奖的奖品价值为X,求X的分布列及数学期望EX.
(1)求同行的两位游客中一人获一等奖、一人获二等奖的概率;
(2)设一位游客在该景点处获奖的奖品价值为X,求X的分布列及数学期望EX.
考点:离散型随机变量的期望与方差,离散型随机变量及其分布列
专题:概率与统计
分析:(1)一位游客获一等奖的概率为p1=
,获二等奖的概率为p2=
,由此能求出两位游客中一人获一等奖、一人获二等奖的概率.
(2)由已知得X可取0、20、60、120,分别求出相应的概率,由此能求出X的分布列的EX.
| 1 |
| 36 |
| 5 |
| 36 |
(2)由已知得X可取0、20、60、120,分别求出相应的概率,由此能求出X的分布列的EX.
解答:
解:(1)一位游客获一等奖的概率为p1=
,
获二等奖的概率为p2=
,
故两位游客中一人获一等奖、一人获二等奖的概率为:
•
•
=
.…(5分)
(2)由已知得X可取0、20、60、120,
则P(X=0)=
,
P(X=20)=
,
P(X=60)=
,
P(X=120)=
,
∴X的分布列为
EX=0×
+20×
+60×
+120×
=
.
| 1 |
| 36 |
获二等奖的概率为p2=
| 5 |
| 36 |
故两位游客中一人获一等奖、一人获二等奖的概率为:
| C | 1 2 |
| 1 |
| 36 |
| 5 |
| 36 |
| 5 |
| 648 |
(2)由已知得X可取0、20、60、120,
则P(X=0)=
| 7 |
| 12 |
P(X=20)=
| 1 |
| 4 |
P(X=60)=
| 5 |
| 36 |
P(X=120)=
| 1 |
| 36 |
∴X的分布列为
| X | 0 | 20 | 60 | 120 | ||||||||
| P |
|
|
|
|
| 7 |
| 12 |
| 1 |
| 4 |
| 5 |
| 36 |
| 1 |
| 36 |
| 50 |
| 3 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题.

练习册系列答案
相关题目
下列说法中正确的是( )
A、
| ||||||||
B、若
| ||||||||
C、若
| ||||||||
D、若
|
 在长方体OABC-O1A1B1C1中,|OA|=2,|AB|=3,|AA1|=2,E是BC的中点,建立空间直角坐标系,用向量方法解决下列问题.
在长方体OABC-O1A1B1C1中,|OA|=2,|AB|=3,|AA1|=2,E是BC的中点,建立空间直角坐标系,用向量方法解决下列问题.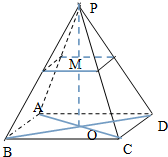 如图,已知四棱锥P-ABCD的底边长与侧棱的长度都是4,ABCD是正方形.
如图,已知四棱锥P-ABCD的底边长与侧棱的长度都是4,ABCD是正方形. 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=2AB=2,E是线段PD上的点.
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=2AB=2,E是线段PD上的点.