题目内容
6．设$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$均为非零向量，则$\overrightarrow{a}$=$\overrightarrow{c}$是$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{b}$•$\overrightarrow{c}$的（ ）| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
分析 $\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$均为非零向量，$\overrightarrow{a}$•$\overrightarrow{c}$=$\overrightarrow{b}$•$\overrightarrow{c}$?（$\overrightarrow{a}-\overrightarrow{b}$）$•\overrightarrow{c}$=0，可得$\overrightarrow{a}$=$\overrightarrow{b}$，或（$\overrightarrow{a}-\overrightarrow{b}$）$⊥\overrightarrow{c}$．即可判断出结论．
解答 解：∵$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$均为非零向量，
$\overrightarrow{a}$•$\overrightarrow{c}$=$\overrightarrow{b}$•$\overrightarrow{c}$?（$\overrightarrow{a}-\overrightarrow{b}$）$•\overrightarrow{c}$=0，∴$\overrightarrow{a}$=$\overrightarrow{b}$，或（$\overrightarrow{a}-\overrightarrow{b}$）$⊥\overrightarrow{c}$．
∴$\overrightarrow{a}$=$\overrightarrow{b}$是$\overrightarrow{a}$•$\overrightarrow{c}$=$\overrightarrow{b}$•$\overrightarrow{c}$的充分不必要条件．
故选：A．
点评 本题考查了向量垂直与数量积的关系、简易逻辑的判定方法，考查了推理能力与计算能力，属于中档题．
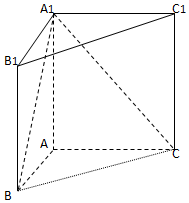如图，直三棱柱ABC-A1B1C1中，AB=1，AC=AA1=$\sqrt{3}$，∠ABC=60°．
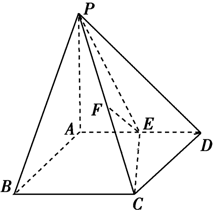如图所示，在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD为正方形，且PA=AD=2，E、F分别为棱AD、PC的中点．| A． | Y～N（aμ，σ2） | B． | Y～N（0，1） | C． | Y～N（$\frac{μ}{a}$，$\frac{σ2}{b}$） | D． | Y～N（aμ+b，a2σ2） |