题目内容
9.某舰艇在A处测得遇险渔船在北偏东45°方向上的C处,且到A的距离为10海里,此时得知,该渔船沿南偏东75°方向,以每小时9海里的速度向一小岛靠近,舰艇的速度为21海里/小时,则舰艇到达渔船的最短时间是$\frac{2}{3}$小时.分析 设两船在B点相遇,设舰艇到达渔船的最短时间是x小时,由题设知AC=10,AB=21x,BC=9x,∠ACB=120°,由余弦定理,知(21x)2=100+(9x)2-2×10×9x×cos120°,由此能求出舰艇到达渔船的最短时间.
解答 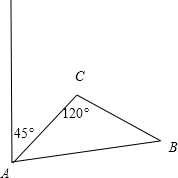 解:设两船在B点相遇,由题设作出图形,
解:设两船在B点相遇,由题设作出图形,
设舰艇到达渔船的最短时间是x小时,
则AC=10,AB=21x,BC=9x,∠ACB=120°,
由余弦定理,知(21x)2=100+(9x)2-2×10×9x×cos120°,
整理,得36x2-9x-10=0,
解得x=$\frac{2}{3}$,或x=-$\frac{5}{12}$(舍).
答:舰艇到达渔船的最短时间是$\frac{2}{3}$小时.
故答案为:$\frac{2}{3}$.
点评 本题考查解三角形在生产实际中的应用,考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.综合性强,是高考的重点,易错点是知识体系不牢固.解题时要注意余弦定理和数形结合思想的灵活运用.

练习册系列答案
相关题目
20.已知直线且l:mx+y+3m-$\sqrt{3}$=0与圆x2+y2=12交于A,B两点,过A,B分别作l的垂线与x轴交于C,D两点,若|AB|=2$\sqrt{3}$,则|CD|=( )
| A. | 4 | B. | 6 | C. | 2$\sqrt{3}$ | D. | 2$\sqrt{2}$ |
19.若a>1,则不等式|x|+a>1的解集是( )
| A. | {x|a-1<x<1-a} | B. | {x|x<a-1或x>1-a} | C. | ∅ | D. | R |
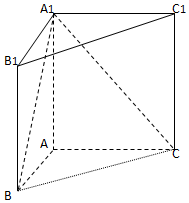 如图,直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=$\sqrt{3}$,∠ABC=60°.
如图,直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=$\sqrt{3}$,∠ABC=60°.