题目内容
7.设A,B分别是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右顶点,P是双曲线C上异于A,B的任一点,设直线AP,BP的斜率分别为m,n,则$\frac{2a}{b}$+ln|m|+ln|n|取得最小值时,双曲线C的离心率为( )| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $\sqrt{6}$ |
分析 由题意求得直线AP及PB斜率,根据对数的运算性质即可求得ln|m|+ln|n|=ln丨mn丨=ln$\frac{{b}^{2}}{{a}^{2}}$,构造函数,求导,根据函数的单调性即可求得t=1时,h(t)取最小值,$\frac{b}{a}$=1,利用双曲线的离心率公式即可求得答案.
解答 解:由A(-a,0),B(a,0),设P(x0,y0),则$\frac{{x}_{0}^{2}}{{a}^{2}}-\frac{{y}_{0}^{2}}{{b}^{2}}=1$,y02=$\frac{{b}^{2}({x}_{0}^{2}-{a}^{2})}{{a}^{2}}$,
则m=$\frac{{y}_{0}}{{x}_{0}+a}$,n=$\frac{{y}_{0}}{{x}_{0}-a}$,则mn=$\frac{{y}_{0}^{2}}{{x}_{0}^{2}-{a}^{2}}$=$\frac{{b}^{2}}{{a}^{2}}$,
ln|m|+ln|n|=ln丨mn丨=ln$\frac{{b}^{2}}{{a}^{2}}$,
$\frac{2a}{b}$+ln|m|+ln|n|=$\frac{2a}{b}$+ln$\frac{{b}^{2}}{{a}^{2}}$,
设$\frac{b}{a}$=t,t>0,
则h(t)=$\frac{2}{t}$+2lnt,t>0,
h′(t)=$\frac{2}{t}$-$\frac{2}{{t}^{2}}$=$\frac{2(t-1)}{{t}^{2}}$,
则t=1时,h(t)取最小值,
∴则$\frac{b}{a}$=1,
则双曲线的离心率e=$\frac{c}{a}$=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$=$\sqrt{2}$,
∴双曲线C的离心率$\sqrt{2}$,
故选:C.
点评 本题考查双曲线的简单几何性质,对数的运算性质,导数与函数单调性及最值的关系,考查计算能力,属于中档题.

| A. | 0个 | B. | 1个 | C. | 2个 | D. | 无数个 |
 如图,在平行四边形ABCD中,AB=1,AD=2,点E,F,G,H分别是AB,BC,CD,DA边上的中点,则$\overrightarrow{EF}•\overrightarrow{FG}+\overrightarrow{GH}•\overrightarrow{HE}$=( )
如图,在平行四边形ABCD中,AB=1,AD=2,点E,F,G,H分别是AB,BC,CD,DA边上的中点,则$\overrightarrow{EF}•\overrightarrow{FG}+\overrightarrow{GH}•\overrightarrow{HE}$=( )| A. | $\frac{3}{2}$ | B. | $-\frac{3}{2}$ | C. | $\frac{3}{4}$ | D. | $-\frac{3}{4}$ |
 如图,已知直角梯形ABCD所在的平面垂直于平面ABE,∠EAB=∠ABC=90°,∠DAB=60°,AB=AD=AE,P为线段BE的中点.
如图,已知直角梯形ABCD所在的平面垂直于平面ABE,∠EAB=∠ABC=90°,∠DAB=60°,AB=AD=AE,P为线段BE的中点.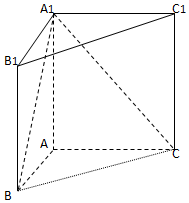 如图,直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=$\sqrt{3}$,∠ABC=60°.
如图,直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=$\sqrt{3}$,∠ABC=60°.