题目内容
5.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的右焦点为F,上顶点为A,若直线AF与圆O:${x^2}+{y^2}=\frac{{3{a^2}}}{16}$相切,则该椭圆的离心率为( )| A. | $\frac{{\sqrt{3}}}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{1}{2}$或$\frac{{\sqrt{3}}}{2}$ |
分析 求得直线AF的方程,利用点到直线的距离公式,利用椭圆离心率公式,即可求得椭圆的离心率.
解答 解:直线AF的方程为$\frac{x}{c}+\frac{y}{b}=1$,即bx+cy-bc=0,
圆心O到直线AF的距离$d=\frac{{|{-bc}|}}{{\sqrt{{b^2}+{c^2}}}}=\frac{bc}{a}=\frac{{\sqrt{3}}}{4}a$,
两边平方整理得,16(a2-c2)c2=3a4,
于是16(1-e2)e2=3,解得${e^2}=\frac{1}{4}$或${e^2}=\frac{3}{4}$.
则e=$\frac{1}{2}$或e=$\frac{\sqrt{3}}{2}$,
故选:D.
点评 本题考查椭圆的标准方程及简单几何性质,点到直线的距离公式,考查计算能力,属于中档题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案
相关题目
20.已知直线且l:mx+y+3m-$\sqrt{3}$=0与圆x2+y2=12交于A,B两点,过A,B分别作l的垂线与x轴交于C,D两点,若|AB|=2$\sqrt{3}$,则|CD|=( )
| A. | 4 | B. | 6 | C. | 2$\sqrt{3}$ | D. | 2$\sqrt{2}$ |
10.已知$\frac{1-tanα}{1+tanα}$=2+$\sqrt{3}$,则tan($\frac{π}{4}$+α)等于( )
| A. | 2+$\sqrt{3}$ | B. | 1 | C. | 2-$\sqrt{3}$ | D. | $\sqrt{3}$ |
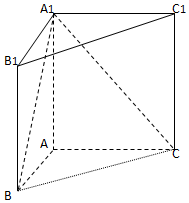 如图,直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=$\sqrt{3}$,∠ABC=60°.
如图,直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=$\sqrt{3}$,∠ABC=60°.