题目内容
11.已知集合A={x|x2-8x+12≤0},B={x|5-2m≤x≤m+1}.(1)当m=3时,求集合A∩B,A∪B;
(2)若B⊆A,求实数m的取值范围.
分析 (1)将m=3代入求出B,求出A,从而求出A∩B,A∪B即可;(2)根据B⊆A,通过讨论B=∅和B≠∅时得到关于m的不等式组,解出即可.
解答 解:(1)当m=3时,B={x|5-6≤x≤3+1}=[-1,4](1分)
因为A={x|2≤x≤6}(3分)
所以A∩B=[2,4](4分)A∪B=[-1,6](5分)
(2)因为B⊆A,所以当B=∅时,5-2m>m+1(6分)
所以$m<\frac{4}{3}$(7分)
当B≠∅时,则$\left\{\begin{array}{l}5-2m≤m+1\\ 5-2m≥2\\ m+1≤6\end{array}\right.$(8分)
解得$\frac{4}{3}≤m≤\frac{3}{2}$(9分)
综上所述:实数m的取值范围为$m≤\frac{3}{2}$(10分)
点评 本题考查了集合的包含关系,考查集合的交集.并集的运算,是一道基础题.

练习册系列答案
相关题目
1.如图是一个四棱锥的三视图,则该几何体的体积为( )


| A. | 16 | B. | 12 | C. | 9 | D. | 8 |
19.某市政府为了确定一个较为合理的居民用电标准,必须先了解全市 居民日常用电量的分布情况.现采用抽样调查的方式,获得了n位居民在2015年的月均用电量(单位:度)数据,样本统计结果如图表:
(1)求n的值和月均用电量的平均数估计值;
(2)如果用分层抽样的方法从用电量小于30度的居民中抽取5位居民,再从这5位居民中选2人,那么至少有1位居民月均用电量在20至30度的概率是多少?
(1)求n的值和月均用电量的平均数估计值;
(2)如果用分层抽样的方法从用电量小于30度的居民中抽取5位居民,再从这5位居民中选2人,那么至少有1位居民月均用电量在20至30度的概率是多少?
| 分组 | 频数 | 频率 |
| [0,10) | 0.05 | |
| [10,20) | 0.10 | |
| [20,30) | 30 | |
| [30,40) | 0.25 | |
| [40,50) | 0.15 | |
| [50,60] | 15 | |
| 合计 | n | 1 |
6.已知集合A={1,2,3},则B={x-y|x∈A,y∈A}中的元素个数为( )
| A. | 9 | B. | 5 | C. | 3 | D. | 1 |
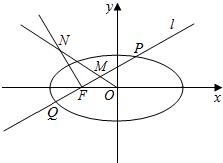 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(0,$\sqrt{2}$),离心率为$\frac{\sqrt{6}}{3}$,点O为坐标原点.
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(0,$\sqrt{2}$),离心率为$\frac{\sqrt{6}}{3}$,点O为坐标原点.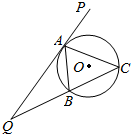 如图,△ABC的外接圆为⊙O,延长CB至Q,再延长QA至P,且QA为⊙O的切线
如图,△ABC的外接圆为⊙O,延长CB至Q,再延长QA至P,且QA为⊙O的切线