题目内容
设函数f(x)=
,则使得f(x)≤2成立的x的取值范围是 .
|
考点:其他不等式的解法,分段函数的解析式求法及其图象的作法
专题:计算题,函数的性质及应用
分析:利用分段函数,结合f(x)≤2,解不等式,即可求出使得f(x)≤2成立的x的取值范围.
解答:
解:x<1时,ex-1≤2,
∴x≤ln2+1,
∴x<1;
x≥1时,x
≤2,
∴x≤8,
∴1≤x≤8,
综上,使得f(x)≤2成立的x的取值范围是x≤8.
故答案为:x≤8.
∴x≤ln2+1,
∴x<1;
x≥1时,x
| 1 |
| 3 |
∴x≤8,
∴1≤x≤8,
综上,使得f(x)≤2成立的x的取值范围是x≤8.
故答案为:x≤8.
点评:本题考查不等式的解法,考查分段函数,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
若log4(3a+4b)=log2
,则a+b的最小值是( )
| ab |
A、6+2
| ||
B、7+2
| ||
C、6+4
| ||
D、7+4
|
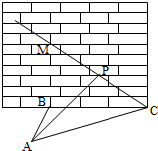 如图,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练.已知点A到墙面的距离为AB,某目标点P沿墙面上的射线CM移动,此人为了准确瞄准目标点P,需计算由点A观察点P的仰角θ的大小.若AB=15m,AC=25m,∠BCM=30°,则tanθ的最大值是
如图,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练.已知点A到墙面的距离为AB,某目标点P沿墙面上的射线CM移动,此人为了准确瞄准目标点P,需计算由点A观察点P的仰角θ的大小.若AB=15m,AC=25m,∠BCM=30°,则tanθ的最大值是