题目内容
分别在区间[1,6]和[1,4]内任取一个实数,依次记为m和n,则m>n的概率为 .
考点:几何概型
专题:计算题,概率与统计
分析:由题意知本题是一个几何概型,根据所给的条件作出试验发生是包含的所有事件是一个矩形区域,做出面积,看出满足条件的事件对应的面积,根据几何概型公式得到结果.
解答:
 解:由题意,(m,n)表示的图形面积为(4-1)×(6-1)=15,其中满足m>n的图形面积为
解:由题意,(m,n)表示的图形面积为(4-1)×(6-1)=15,其中满足m>n的图形面积为
×(2+5)×3=
,
故m>n的概率为
=
.
故答案为:
.
 解:由题意,(m,n)表示的图形面积为(4-1)×(6-1)=15,其中满足m>n的图形面积为
解:由题意,(m,n)表示的图形面积为(4-1)×(6-1)=15,其中满足m>n的图形面积为| 1 |
| 2 |
| 21 |
| 2 |
故m>n的概率为
| ||
| 15 |
| 7 |
| 10 |
故答案为:
| 7 |
| 10 |
点评:古典概型和几何概型是我们学习的两大概型,古典概型要求能够列举出所有事件和发生事件的个数,而不能列举的就是几何概型,几何概型的概率的值是通过长度、面积、和体积、的比值得到.

练习册系列答案
相关题目
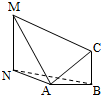 如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点,从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°,以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=100m,则山高MN=
如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点,从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°,以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=100m,则山高MN=