题目内容
1.已知a,b是实数,函数f(x)=x|x-a|+b.(1)当a=2时,求函数f(x)的单调区间;
(2)当a>0时,求函数f(x)在区间[1,2]上的最大值;
(3)若存在a∈[-3,0],使得函数f(x)在[-4,5]上恒有三个零点,求b的取值范围.
分析 (1)当a=2时,作出函数f(x)的表达式,利用数形结合即可求函数f(x)的单调区间;
(2)当a>0时,先求出f(1)=f(2),然后利用数形结合即可函数f(x)在区间[1,2]上的最大值;
(3)利用参数分离法将条件进行转化,利用数形结合即可求b的取值范围.
解答 解:(1)当a=2时,f(x)=x|x-2|+b=$\left\{\begin{array}{l}{{x}^{2}-2x+b,}&{x≥2}\\{-{x}^{2}+2x+b,}&{x<2}\end{array}\right.$,
由二次函数的单调性知,
f(x)在(-∞,1]上单调递增,在(1,2)上单调递减,在[2,+∞)上单调递增.
(2)设g(x)=x|x-a|=$\left\{\begin{array}{l}{{x}^{2}-ax=(x-\frac{a}{2})^{2}-\frac{{a}^{2}}{4},x≥a}\\{ax-{x}^{2}=-(x-\frac{a}{2})^{2}+\frac{{a}^{2}}{4},x<a}\end{array}\right.$,
由于a>0且1≤x≤2,结合函数f(x)的图象可知,
若f(1)=f(2),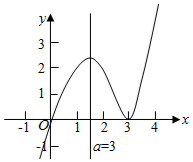
即g(1)=g(2),
则|1-a|=2|2-a|,
平方得1-2a+a2=16-16a+4a2,
即3a2-14a+15=0,
得a=3或a=$\frac{5}{3}$,
当0<a≤$\frac{5}{3}$时,g(2)≥g(1),此时g(2)最大,即f(2)最大,最大值为f(2)=2|2-a|+b=4-2a+b,
若$\frac{5}{3}$<a<3时,g(2)<g(1),此时g(1)最大,
即f(1)最大,最大值为f(1)=|1-a|+b=1-a+b,
若a≥3时,g(2)>g(1),此时g(2)最大,
即f(2)最大,最大值为f(2)=2|2-a|+b=2a-4+b,
(3)若存在a∈[-3,0],使得函数f(x)在[-4,5]上恒有三个零点,
则存在a∈[-3,0],使得b=-x|x-a|有三个不同的实根;
令g(x)=-x|x-a|=$\left\{\begin{array}{l}{-{x}^{2}+ax,}&{x≥a}\\{{x}^{2}-ax,}&{x<a}\end{array}\right.$,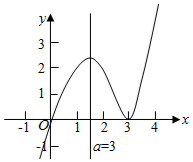
(ⅰ)当a=0时,g(x)在[-4,5]上单调递减,故b无解;
(ⅱ)当-3≤a<0时,g(x)在(-∞,a)上单调递减,在[a,$\frac{a}{2}$]上单调递增,在($\frac{a}{2}$,+∞)上单调递减,
∵g(-4)=4|4+a|=16+4a,g(a)=0,g($\frac{a}{2}$)=$\frac{{a}^{2}}{4}$,g(5)=5a-25,
∴g(-4)-g($\frac{a}{2}$)=$\frac{-(a-8)^{2}+128}{4}$>0,g(a)-g(5)=25-5a>0,
∴0<b<$\frac{{a}^{2}}{4}$,
∴0<b<$\frac{9}{4}$.
点评 本题考查了分段函数的应用及二次函数的单调性的应用,同时考查了分类讨论的思想应用,综合性较强,难度较大.

 定义在R上的可导函数f(x)的导函数为f′(x),已知函数y=2f′(x)的图象如图所示,则函数y=f(x)的单调递减区间为( )
定义在R上的可导函数f(x)的导函数为f′(x),已知函数y=2f′(x)的图象如图所示,则函数y=f(x)的单调递减区间为( )| A. | (1,+∞) | B. | (1,2) | C. | (-∞,2) | D. | (2,+∞) |
| A. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1 | B. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{25}$=1 | C. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1 | D. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{25}$=1 |
| A. | x=-$\frac{π}{2}$ | B. | x=-$\frac{π}{4}$ | C. | x=$\frac{π}{8}$ | D. | x=$\frac{π}{4}$ |
| A. | 210 | B. | 120 | C. | 90 | D. | 80 |