题目内容
9.已知圆C:x2+(y-4)2=100,点A为圆C上的动点,点B的坐标为(0,-4),动点P满足$\overrightarrow{CP}$=$λ\overrightarrow{PA}$(λ>0),($\overrightarrow{OA}$+$\overrightarrow{OB}$-2$\overrightarrow{OP}$)•($\overrightarrow{OA}$-$\overrightarrow{OB}$)=0,则点P的轨迹方程为( )| A. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1 | B. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{25}$=1 | C. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1 | D. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{25}$=1 |
分析 作出圆的图象,根据向量数量积的定义判断,P的轨迹是以C,B为焦点的椭圆,求出a,b,即可得到结论.
解答 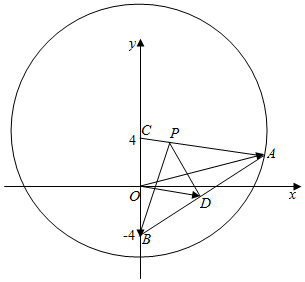 解:作出圆的图象如图,则C(0,4),
解:作出圆的图象如图,则C(0,4),
∵点A为圆C上的动点,
∴CA=R=10,
∵是D是AB的中点,
∴由($\overrightarrow{OA}$+$\overrightarrow{OB}$-2$\overrightarrow{OP}$)•($\overrightarrow{OA}$-$\overrightarrow{OB}$)=0得(2$\overrightarrow{OD}$-2$\overrightarrow{OP}$)•$\overrightarrow{BA}$=0,
即2$\overrightarrow{PD}$•$\overrightarrow{BA}$=0,
则PD⊥AB,
∵D是AB的中点,
∴△ABP是等腰三角形,
则PD=PB,
∵CA=CP+PAR=CP+PB=10>AB=8,
∴P的轨迹是以C,B为焦点的椭圆,
则c=4,2a=10,即a=5,则b2=a2-c2=25-16=9,
即点P的轨迹方程为$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{25}$=1,
故选:D
点评 本题主要考查点的轨迹方程的求解,结合向量数量积的应用,转化为椭圆的定义是解决本题的关键.综合性较强,有一定的难度.

练习册系列答案
相关题目
2.实轴长是10,焦点坐标分别为(0,-$\sqrt{29}$),(0,$\sqrt{29}$)的双曲线方程为( )
| A. | $\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{4}$=1 | B. | $\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{25}$=1 | C. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{25}$=1 | D. | $\frac{{y}^{2}}{25}$-$\frac{{x}^{2}}{4}$=1 |
4.函数f(x)=sin(x+$\frac{π}{6}$)-$\sqrt{3}$sin($\frac{π}{3}$-x)(x∈R)的最大值为( )
| A. | 1+$\sqrt{3}$ | B. | 2 | C. | 1 | D. | -1+$\sqrt{3}$ |
14.已知AB是单位圆上的动点,且|AB|=$\sqrt{3}$、单位圆的圆心为O,则$\overrightarrow{OA}•\overrightarrow{OB}$=( )
| A. | -$\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |