题目内容
11．将A，B，C共3本不同的书放到6个书柜里面，若每个书柜最多放2本，则不同的放法种数是（ ）| A． | 210 | B． | 120 | C． | 90 | D． | 80 |
分析 利用间接法，先求出将A，B，C共3本不同的书放到6个书柜里面的放法，再排除每个书柜放3本，问题得以解决．
解答 解：将A，B，C共3本不同的书放到6个书柜里面，每本书都有6种放法，
根据乘法原理可得不同放法为63=216种，其中每个书柜放3本，有6个不同的方法，
故每个书柜最多放2本，则不同的放法种数是216-6=210，
故选：A．
点评 本题考查分步乘法计数原理，考查学生的计算能力，比较基础．
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
课课优能力培优100分系列答案
相关题目
2．将函数f（x）=sin（2x+φ）$（|φ|＜\frac{π}{2}）$的图象向右平移$\frac{π}{12}$个单位后的图象关于y轴对称，则函数f（x）在$[0，\frac{π}{2}]$上的最小值为（ ）
| A． | $\frac{{\sqrt{3}}}{2}$ | B． | $\frac{1}{2}$ | C． | $-\frac{1}{2}$ | D． | $-\frac{{\sqrt{3}}}{2}$ |
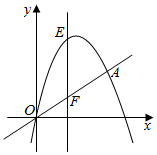如图所示，已知二次函数y=-x2+4x+c的图象经过坐标原点，并且与函数y=x的图象交于O，A两点．求：