题目内容
13．函数f（x）=$\sqrt{1-{x}^{2}}$的定义域是[-1，1]．分析 根据二次根式的性质求出函数的定义域即可．
解答 解：由题意得：1-x2≥0，
解得：-1≤x≤1，
故函数的定义域是：[-1，1]，
故答案为：[-1，1]．
点评 本题考查了求函数的定义域问题，考查解不等式问题，是一道基础题．
练习册系列答案
相关题目
3．已知圆C：（x+c）2+y2=4a2，点A（c，0），其中c＞a＞0，M是圆C上的动点，MA的中垂线交MC所在直线于P，则点P的轨迹是（ ）
| A． | 椭圆 | B． | 双曲线 | C． | 抛物线 | D． | 直线 |
4．函数f（x）=sin（x+$\frac{π}{6}$）-$\sqrt{3}$sin（$\frac{π}{3}$-x）（x∈R）的最大值为（ ）
| A． | 1+$\sqrt{3}$ | B． | 2 | C． | 1 | D． | -1+$\sqrt{3}$ |
8．已知集合A={x∈R|1≤x≤5}，B={x∈R|x＜2}，则A∩B为（ ）
| A． | {x∈R|1≤x＜2} | B． | {x∈R|x＜1} | C． | {x∈R|2＜x≤5} | D． | {x∈R|2≤x≤5} |
5．设集合A={x|x2-4＜0}，B={1，2，3}，则A∩B=（ ）
| A． | {1，2，3} | B． | {1，2} | C． | {1} | D． | {2} |
2．将函数f（x）=sin（2x+φ）$（|φ|＜\frac{π}{2}）$的图象向右平移$\frac{π}{12}$个单位后的图象关于y轴对称，则函数f（x）在$[0，\frac{π}{2}]$上的最小值为（ ）
| A． | $\frac{{\sqrt{3}}}{2}$ | B． | $\frac{1}{2}$ | C． | $-\frac{1}{2}$ | D． | $-\frac{{\sqrt{3}}}{2}$ |
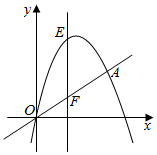如图所示，已知二次函数y=-x2+4x+c的图象经过坐标原点，并且与函数y=x的图象交于O，A两点．求：