题目内容
17．已知函数f（x）=$\left\{\begin{array}{l}{x^2}，x≤a\\ 2x+3，x＞a\end{array}$，若方程f（x）+2x-8=0恰有两个不同实根，则实数a的取值范围是（ ）| A． | $[-4，\frac{5}{4}]∪[2，+∞）$ | B． | [-4，2] | C． | $（\frac{5}{4}，2]$ | D． | $[{-4，\frac{5}{4}}]$ |
分析 函数f（x）的图象与函数y=-2x+8共有两个交点，可能为：两个交点均为y=-2x+8与二次函数y=x2的交点，也可能为：两个交点为y=-2x+8与y=2x+3的交点，另一个是y=-2x+8与二次函数y=x2的交点，进而得到答案．
解答 解：y=x2与y=-2x+8共有两个交点（-4，16），（2，4），
y=2x+3与y=-2x+8有一个交点（$\frac{5}{4}$，$\frac{11}{2}$），
若方程f（x）+2x-8=0恰有两个不同实根，
则函数f（x）的图象与函数y=-2x+8共有两个交点，
若两个交点均为y=-2x+8与二次函数y=x2的交点，则a≥2，
若两个交点为y=-2x+8与y=2x+3的交点，另一个是y=-2x+8与二次函数y=x2的交点，则-4≤a≤$\frac{5}{4}$，
综相所述，a∈$[-4，\frac{5}{4}]∪[2，+∞）$，
故选：A．
点评 本题考查的知识点是根的存在性及根的个数判断，分段函数的应用，难度中档．
练习册系列答案
心算口算巧算一课一练系列答案
应用题作业本系列答案
相关题目
18．焦点在x轴上的椭圆C：$\frac{{x}^{2}}{{a}^{2}}+{y}^{2}$=1，过右焦点作垂直于x轴的直线交椭圆与A，B两点，且|AB|=1，则该椭圆的离心率为（ ）
| A． | $\frac{\sqrt{3}}{2}$ | B． | $\frac{1}{2}$ | C． | $\frac{\sqrt{15}}{4}$ | D． | $\frac{\sqrt{5}}{3}$ |
5．已知函数f（x）=-x3-x+sinx，若关于x的不等式$f（\frac{1}{x}）+f（x-m）＞0$在$[\frac{1}{2}，2]$上有解，则实数m的取值范围是（ ）
| A． | $m＜\frac{5}{2}$ | B． | $m＞\frac{5}{2}$ | C． | m＜2 | D． | m＞2 |
12．{an}是各项均为正数的等差数列，{bn}是等比数列，已知$\frac{a_1}{b_1}$=$\frac{a_2}{b_2}$=1，$\frac{a_3}{b_3}$=$\frac{8}{9}$，那么$\frac{a_4}{b_4}$=（ ）
| A． | $\frac{20}{27}$ | B． | $\frac{16}{27}$ | C． | $\frac{4}{9}$ | D． | $\frac{20}{27}$或$\frac{16}{27}$ |
9．设a=log${\;}_{\frac{1}{3}}}$2，b=20.6，c=log43，则a，b，c的大小关系为（ ）
| A． | a＞b＞c | B． | c＞b＞a | C． | b＞c＞a | D． | a＞c＞b |
6．一个底面为正方形的棱锥的三视图如图所示，则它的外接球的表面积为（ ）
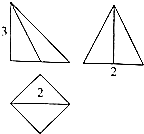
| A． | $\frac{13π}{4}$ | B． | $\frac{{\sqrt{13}π}}{2}$ | C． | 13π | D． | $\sqrt{13}π$ |