题目内容
9.设a=log${\;}_{\frac{1}{3}}}$2,b=20.6,c=log43,则a,b,c的大小关系为( )| A. | a>b>c | B. | c>b>a | C. | b>c>a | D. | a>c>b |
分析 根据指数函数的图象和性质,对数函数的图象和性质,逐一分析a,b,c的大小,可得答案.
解答 解:a=log${\;}_{\frac{1}{3}}}$2<0,b=20.6>1,0<c=log43<1,
故b>c>a,
故选:C.
点评 本题考查的知识点是利用指数函数的图象和性质,对数函数的图象和性质,比较数的大小,难度中档.

练习册系列答案
相关题目
17.已知函数f(x)=$\left\{\begin{array}{l}{x^2},x≤a\\ 2x+3,x>a\end{array}$,若方程f(x)+2x-8=0恰有两个不同实根,则实数a的取值范围是( )
| A. | $[-4,\frac{5}{4}]∪[2,+∞)$ | B. | [-4,2] | C. | $(\frac{5}{4},2]$ | D. | $[{-4,\frac{5}{4}}]$ |
1.程序如图,要使此程序能运算出“1+2+…+100”的结果,需将语句“i=i+1”加在( ) 

| A. | ①处 | B. | ②处 | C. | ③处 | D. | ④处 |
18.已知f(x)=$\left\{{\begin{array}{l}{{x^2}-1,(x>0)}\\{f(x+1)-1,(x≤0)}\end{array}}$,则f(-1)=( )
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
19.如图,已知一个八面体的各条棱长均为1,四边形ABCD 为正方形,则下列命题中的假命题是( )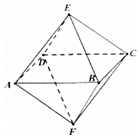

| A. | 不平行的两条棱所在的直线所成的角是60o或90o | |
| B. | 四边形AECF是正方形 | |
| C. | 点A到平面BCE的距离为$\frac{\sqrt{6}}{3}$ | |
| D. | 该八面体的顶点不会在同一个球面上. |