题目内容
18.焦点在x轴上的椭圆C:$\frac{{x}^{2}}{{a}^{2}}+{y}^{2}$=1,过右焦点作垂直于x轴的直线交椭圆与A,B两点,且|AB|=1,则该椭圆的离心率为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{15}}{4}$ | D. | $\frac{\sqrt{5}}{3}$ |
分析 由焦点在x轴的椭圆方程:$\frac{{x}^{2}}{{a}^{2}}+{y}^{2}$=1,焦点在x轴上,即a2>1,c2=a2-1,c=$\sqrt{{a}^{2}-1}$,过右焦点作垂直于x轴的直线交椭圆与A,B两点,丨AB丨为椭圆的通径,则∴|AB|=2丨y丨=1,即可求得a的值,则c=$\sqrt{{a}^{2}-1}$=$\sqrt{3}$,e=$\frac{c}{a}$,即可求得椭圆的离心率.
解答 解:焦点在x轴的椭圆方程:$\frac{{x}^{2}}{{a}^{2}}+{y}^{2}$=1,焦点在x轴上,
即a2>1,c2=a2-1,c=$\sqrt{{a}^{2}-1}$,
右焦点F($\sqrt{{a}^{2}-1}$,0),
过右焦点作垂直于x轴的直线交椭圆与A,B两点,
AB为椭圆的通径,
∴当x=$\sqrt{{a}^{2}-1}$,解得:y=±$\frac{1}{a}$,
∴|AB|=2丨y丨=1,即$\frac{2}{a}$=1,解得:a=2,
则c=$\sqrt{{a}^{2}-1}$=$\sqrt{3}$,
椭圆的离心率e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,
故选A.
点评 本题考查椭圆的标准方程,考查椭圆的焦点坐标公式,考查椭圆通径的应用,考查计算能力,属于基础题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
17.已知函数f(x)=$\left\{\begin{array}{l}{x^2},x≤a\\ 2x+3,x>a\end{array}$,若方程f(x)+2x-8=0恰有两个不同实根,则实数a的取值范围是( )
| A. | $[-4,\frac{5}{4}]∪[2,+∞)$ | B. | [-4,2] | C. | $(\frac{5}{4},2]$ | D. | $[{-4,\frac{5}{4}}]$ |
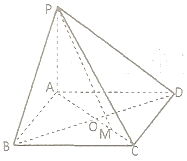 如图,已知四棱锥P-ABCD中,PA⊥BD,底面ABCD是边长为a的菱形,∠BAD=120°,PA=b,AC与BD交于点O,M为OC的中点.
如图,已知四棱锥P-ABCD中,PA⊥BD,底面ABCD是边长为a的菱形,∠BAD=120°,PA=b,AC与BD交于点O,M为OC的中点.