题目内容
12.{an}是各项均为正数的等差数列,{bn}是等比数列,已知$\frac{a_1}{b_1}$=$\frac{a_2}{b_2}$=1,$\frac{a_3}{b_3}$=$\frac{8}{9}$,那么$\frac{a_4}{b_4}$=( )| A. | $\frac{20}{27}$ | B. | $\frac{16}{27}$ | C. | $\frac{4}{9}$ | D. | $\frac{20}{27}$或$\frac{16}{27}$ |
分析 设等差数列{an}的公差为d,等比数列{bn}的公比为q,解得q的值,求出b4,再根据已知条件求出d,则可得到a4,则答案可求.
解答 解:设等差数列{an}的公差为d,等比数列{bn}的公比为q,
则a1+d=a1q,$9({a}_{1}+2d)=8{a}_{1}{q}^{2}$,联立可得8q2-18q+9=0,
解得:q=$\frac{3}{2}$或q=$\frac{3}{4}$.
∵{an}是各项均为正数,则d>0,∴q>1,
则$q=\frac{3}{2}$,
∴${b}_{4}={a}_{1}×(\frac{3}{2})^{3}=\frac{27}{8}{a}_{1}$.
∴$\frac{{a}_{2}}{{b}_{2}}=\frac{3}{2}{a}_{1}$.
则$d=\frac{3}{2}{a}_{1}-{a}_{1}=\frac{1}{2}{a}_{1}$.
∴${a}_{4}={a}_{1}+3d=\frac{5}{2}{a}_{1}$.
∴$\frac{a_4}{b_4}$=$\frac{\frac{5}{2}{a}_{1}}{\frac{27}{8}{a}_{1}}=\frac{20}{27}$.
故选:A.
点评 本题考查了等差等比数列的通项公式,考查等差数列和等比数列的性质,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.已知函数f(x)=$\left\{\begin{array}{l}{x^2},x≤a\\ 2x+3,x>a\end{array}$,若方程f(x)+2x-8=0恰有两个不同实根,则实数a的取值范围是( )
| A. | $[-4,\frac{5}{4}]∪[2,+∞)$ | B. | [-4,2] | C. | $(\frac{5}{4},2]$ | D. | $[{-4,\frac{5}{4}}]$ |
1.程序如图,要使此程序能运算出“1+2+…+100”的结果,需将语句“i=i+1”加在( ) 

| A. | ①处 | B. | ②处 | C. | ③处 | D. | ④处 |
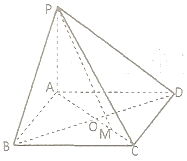 如图,已知四棱锥P-ABCD中,PA⊥BD,底面ABCD是边长为a的菱形,∠BAD=120°,PA=b,AC与BD交于点O,M为OC的中点.
如图,已知四棱锥P-ABCD中,PA⊥BD,底面ABCD是边长为a的菱形,∠BAD=120°,PA=b,AC与BD交于点O,M为OC的中点.