题目内容
f（x）是定义在R上的偶函数，已知函数f（x）在（-∞，0]上单调递减，且f（2）=0，则使f（x）＜0的x的取值范围是（ ）
| A、（-2，0]∪[2，+∞） |
| B、（-2，2） |
| C、（-2，0） |
| D、（2，+∞） |
考点：函数奇偶性的性质,函数单调性的性质
专题：函数的性质及应用
分析：由f（x）为偶函数，f（x）在（-∞，0）上的单调性，可判断f（x）在（0，+∞）上的单调性，由f（2）=0，可得f（-2）=0，从而据题意可作出f（x）的草图，由图象即可解得不等式．
解答：
解：因为f（x）在（-∞，0）上单调递减，又f（x）为R上的偶函数，
所以f（x）在（0，+∞）上单调递增，
由f（2）=0可得f（-2）=0，
作出满足题意的函数f（x）的草图，如图：
由图象可得，使得f（x）＜0的x的范围为（-2，2）．
故选B．
所以f（x）在（0，+∞）上单调递增，
由f（2）=0可得f（-2）=0，
作出满足题意的函数f（x）的草图，如图：
由图象可得，使得f（x）＜0的x的范围为（-2，2）．
故选B．
点评：本题考查函数的奇偶性、单调性及其应用，数形结合解决本题简洁直观，注意体会．
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
根据下列条件解三角形，两解的是（ ）
| A、b=10，A=45°，B=70° |
| B、a=60，c=48，B=100° |
| C、a=14，b=16，A=45° |
| D、a=7，b=5，A=80° |
已知定义在[1，+∞）上的函数f（x）=
，则（ ）
|
| A、函数f（x）的值域为[1，4] | ||
| B、当x∈[2n-1，2n]（n∈N*）时，函数f（x）的图象与x轴围成的面积为2 | ||
C、关于x的方程f（x）-
| ||
| D、存在实数x0，使得不等式x0f（x0）＞6成立 |
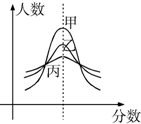某市期末教学质量检测，甲、乙、丙三科考试成绩近似服从正态分布，则由如图曲线可得下列说法中正确的是（ ）| A、甲学科总体的方差最小 |
| B、丙学科总体的均值最小 |
| C、乙学科总体的方差及均值都居中 |
| D、甲、乙、丙的总体的均值不相同 |
已知点P是由不等式组
所确定的平面区域内的动点，点Q是直线2x+y=0上的动点，线段PQ的中点记为M，O为坐标原点，则|OM|的最小值为（ ）
|
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在等差数列{an}中，a2=2，a6=8，则a10的值为（ ）
| A、10 | B、12 | C、14 | D、16 |
已知a=cos234°-sin234°，b=2sin78°cos78°，c=
，则有（ ）
| 2tan12° |
| 1-tan212° |
| A、a＞b＞c |
| B、b＞a＞c |
| C、c＞a＞b |
| D、c＞b＞a |