题目内容
已知a=cos234°-sin234°,b=2sin78°cos78°,c=
,则有( )
| 2tan12° |
| 1-tan212° |
| A、a>b>c |
| B、b>a>c |
| C、c>a>b |
| D、c>b>a |
考点:二倍角的正切,正切函数的单调性
专题:三角函数的求值
分析:由二倍角公式和诱导公式化简可得a=sin22°,b=sin24°,c=tan24°,由三角函数的单调性可得结论.
解答:
解:a=cos234°-sin234°=cos68°=sin22°,
b=2sin78°cos78°=sin156°=sin24°,
c=
=tan24°=
>sin24°=b,
由正弦函数的单调性可知sin24°>sin22°,
∴c>b>a
故选:D
b=2sin78°cos78°=sin156°=sin24°,
c=
| 2tan12° |
| 1-tan212° |
| sin24° |
| cos24° |
由正弦函数的单调性可知sin24°>sin22°,
∴c>b>a
故选:D
点评:本题考查二倍角公式,涉及三角函数的单调性和诱导公式,属中档题.

练习册系列答案
相关题目
在△ABC中的内角A,B,C所对的边分别为a,b,c,若∠B=60°,a,b,c成等比数列,则△ABC的形状为( )
| A、直角三角形 | B、等腰三角形 |
| C、等边三角形 | D、不确定 |
如图是导函数y=f′(x)的图象,那么函数y=f(x)在下面哪个区间是减函数( )
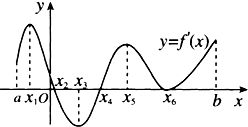

| A、(x1,x3) |
| B、(x2,x4) |
| C、(x4,x6) |
| D、(x5,x6) |
f(x)是定义在R上的偶函数,已知函数f(x)在(-∞,0]上单调递减,且f(2)=0,则使f(x)<0的x的取值范围是( )
| A、(-2,0]∪[2,+∞) |
| B、(-2,2) |
| C、(-2,0) |
| D、(2,+∞) |
下列命题中正确的是( )
| A、若p:?x∈R,x2+x+1<0,则¬p:?x∈R,x2+x+1<0 |
| B、若p∨q为真命题,则p∧q也为真命题 |
| C、命题“若x2-3x+2=0,则x=1”的否命题为真命题 |
| D、“函数f(x)为奇函数”是“f(0)=0”的充分不必要条件 |
已知向量
,
满足:|
|=2,|
|=1,且
•
=2,则|
+
|为( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、3 | B、4 | C、9 | D、8 |
执行所示的程序框图,如果输入N=5,则输出的数等于( )
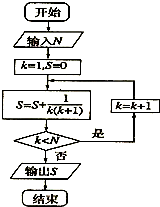

A、
| ||
B、
| ||
C、
| ||
D、
|
