题目内容
已知定义在[1,+∞)上的函数f(x)=
,则( )
|
| A、函数f(x)的值域为[1,4] | ||
| B、当x∈[2n-1,2n](n∈N*)时,函数f(x)的图象与x轴围成的面积为2 | ||
C、关于x的方程f(x)-
| ||
| D、存在实数x0,使得不等式x0f(x0)>6成立 |
考点:分段函数的应用
专题:函数的性质及应用
分析:根据题意,对选项中的每一个问题进行分析与思考,结合函数f(x)的解析式进行解答,即可得出正确的选项.
解答:
解:根据题意,得:
对于A,当1≤x≤2时,0≤|8x-12|≤4,∴0≤4-|8x-12|≤4,∴f(x)的值域为[0,4],∴A选项错误;
对于B,令n=1,由题意知当x∈[1,2]时,函数f(x)的图象与x轴围成的图形是一个三角形,
其面积为S=
×1×4=2,∴B选项正确;
对于C,当n=1时,方程为f(x)=
,此时方程的根不是2+4=6个,∴C选项错误;
对于D,∵f(x)的值域为[0,4],∴不等式x0f(x0)>6不成立,∴D选项错误.
故选:B.
对于A,当1≤x≤2时,0≤|8x-12|≤4,∴0≤4-|8x-12|≤4,∴f(x)的值域为[0,4],∴A选项错误;
对于B,令n=1,由题意知当x∈[1,2]时,函数f(x)的图象与x轴围成的图形是一个三角形,
其面积为S=
| 1 |
| 2 |
对于C,当n=1时,方程为f(x)=
| 1 |
| 2 |
对于D,∵f(x)的值域为[0,4],∴不等式x0f(x0)>6不成立,∴D选项错误.
故选:B.
点评:本题考查了分段函数的应用问题,解题时应对选项中的每一个问题进行分析与思考,以便做出正确的判断,是易错题.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
在△ABC中的内角A,B,C所对的边分别为a,b,c,若∠B=60°,a,b,c成等比数列,则△ABC的形状为( )
| A、直角三角形 | B、等腰三角形 |
| C、等边三角形 | D、不确定 |
已知命题p:?x∈R,ax>0(a>0且a≠1),则( )
| A、¬p:?x∈R,ax≤0 |
| B、¬p:?x∈R,ax>0 |
| C、¬p:?x0∈R,a x0>0 |
| D、¬p:?x0∈R,a x0≤0 |
已知实数x,y满足约束条件
则z=
的最小值为 ( )
|
| 9x |
| 3-y |
| A、27 | ||
B、
| ||
| C、3 | ||
D、
|
函数f(x)=log3(2x+1)的值域为( )
| A、(0,+∞) |
| B、[0,+∞) |
| C、(1,+∞) |
| D、[1,+∞) |
如图是导函数y=f′(x)的图象,那么函数y=f(x)在下面哪个区间是减函数( )
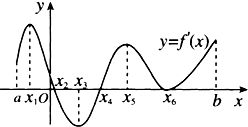

| A、(x1,x3) |
| B、(x2,x4) |
| C、(x4,x6) |
| D、(x5,x6) |
f(x)是定义在R上的偶函数,已知函数f(x)在(-∞,0]上单调递减,且f(2)=0,则使f(x)<0的x的取值范围是( )
| A、(-2,0]∪[2,+∞) |
| B、(-2,2) |
| C、(-2,0) |
| D、(2,+∞) |
