题目内容
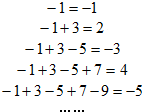 观察如图所示5个等式:照图中式子规律:
观察如图所示5个等式:照图中式子规律:(1)写出第6个等式,并猜想第n个等式;(n∈N*)
(2)用数学归纳法证明上述所猜想的第n个等式成立.(n∈N*)
考点:数学归纳法,归纳推理
专题:点列、递归数列与数学归纳法
分析:(1)通过前5个表达式,直接写出第6个等式,并猜想第n个等式;(n∈N*)
(2)用数学归纳法证明步骤,直接证明上述所猜想的第n个等式成立.(n∈N*)
(2)用数学归纳法证明步骤,直接证明上述所猜想的第n个等式成立.(n∈N*)
解答:
解:(1)第6个等式为-1+3-5+7-9+11=6 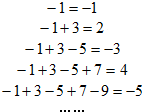
…(2分)
猜想:第n 个等式为-1+3-5+7-9+…+(-1)n•(2n-1)=(-1)n•n …(4分)
(2)下面用数学归纳法给予证明:-1+3-5+7-9+…+(-1)n•(2n-1)=(-1)n•n
①当n=1时,由已知得原式成立; …(5分)
②假设当n=k时,原式成立,
即-1+3-5+7-9+…+(-1)k•(2k-1)=(-1)k•k
…(6分)
那么,当n=k+1时,-1+3-5+7-9+…+(-1)k•(2k-1)+(-1)k+1•(2k+1)
=(-1)k•k+(-1)k+1•(2k+1)=(-1)k+1•(-k+2k+1)=(-1)k+1•(k+1)
故n=k+1时,原式也成立 …(11分)
由①②知,-1+3-5+7-9+…+(-1)n•(2n-1)=(-1)n•n
成立…(13分)
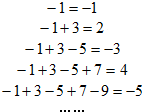
…(2分)
猜想:第n 个等式为-1+3-5+7-9+…+(-1)n•(2n-1)=(-1)n•n …(4分)
(2)下面用数学归纳法给予证明:-1+3-5+7-9+…+(-1)n•(2n-1)=(-1)n•n
①当n=1时,由已知得原式成立; …(5分)
②假设当n=k时,原式成立,
即-1+3-5+7-9+…+(-1)k•(2k-1)=(-1)k•k
…(6分)
那么,当n=k+1时,-1+3-5+7-9+…+(-1)k•(2k-1)+(-1)k+1•(2k+1)
=(-1)k•k+(-1)k+1•(2k+1)=(-1)k+1•(-k+2k+1)=(-1)k+1•(k+1)
故n=k+1时,原式也成立 …(11分)
由①②知,-1+3-5+7-9+…+(-1)n•(2n-1)=(-1)n•n
成立…(13分)
点评:本题考查数学归纳法证明猜想成立,注意证明步骤的应用,缺一不可.

练习册系列答案
相关题目
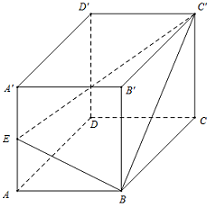 已知正方体ABCD-A′B′C′D′中,E是AA′棱的中点.求平面BEC′与平面ABCD所成的角的余弦值.
已知正方体ABCD-A′B′C′D′中,E是AA′棱的中点.求平面BEC′与平面ABCD所成的角的余弦值.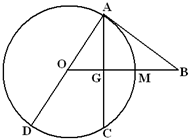 如图,已知AD为圆O的直径,直线BA与圆O相切于点A,直线OB与弦AC垂直并相交于点G,与弧AC相交于M,连接DC,AB=10,AC=12.
如图,已知AD为圆O的直径,直线BA与圆O相切于点A,直线OB与弦AC垂直并相交于点G,与弧AC相交于M,连接DC,AB=10,AC=12. 如图,已知BC为⊙O的直径,点A、F在⊙O上,AD⊥BC,垂足为D,BF交AD于E,且AE=BE.
如图,已知BC为⊙O的直径,点A、F在⊙O上,AD⊥BC,垂足为D,BF交AD于E,且AE=BE. 如图所示,在圆O中,直径AB与弦CD垂直,垂足为E,EF⊥DB,垂足为F,若AB=6,AE=1,求DF•DB的值.
如图所示,在圆O中,直径AB与弦CD垂直,垂足为E,EF⊥DB,垂足为F,若AB=6,AE=1,求DF•DB的值.