题目内容
已知集合A={x|-3≤x＜1}，B={x|a-1＜x≤a}，且A∩B≠∅，则实数a的取值范围是 ．
考点：集合的包含关系判断及应用
专题：集合
分析：本题可以淘汰法思想去研究问题，先考虑A∩B=∅的情况，再求出且A∩B≠∅时的解．
解答：
解：∵集合A={x|-3≤x＜1}，B={x|a-1＜x≤a}，
∴当A∩B=∅时，则有：a＜-3或a-1≥1，即 a＜-3或a≥2．
∴当A∩B≠∅时，则有：-3≤a＜2．
故答案为-3≤a＜2．
∴当A∩B=∅时，则有：a＜-3或a-1≥1，即 a＜-3或a≥2．
∴当A∩B≠∅时，则有：-3≤a＜2．
故答案为-3≤a＜2．
点评：本题考查了集合的交集运算和淘汰法思想，要求学生准确理解交集运算的概念．本题难度较小，属于基础题．
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
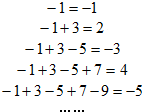观察如图所示5个等式：照图中式子规律：