题目内容
一枚均匀硬币抛掷3次,事件“恰有两次正面向上”的概率为p1,事件“恰有一次反面向上”的概率为p2,已知p1、p2是方程x2+ax+b=0的两个根,求a,b的值.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:首先求出p1、p2,再根据韦大定理求出a、b的值
解答:
解:连续3次抛掷一枚质地均匀的硬币,
恰有两次正面向上”的概率为p1=
•(
)2•
=
,
恰有一次出现反面向上的概率为p2=
•
•(
)2=
,
∵p1、p2是方程x2+ax+b=0的两个根,
∴p1+p2=-a,p1•p2=b
即a=-
,b=
.
恰有两次正面向上”的概率为p1=
| C | 2 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 8 |
恰有一次出现反面向上的概率为p2=
| C | 1 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 8 |
∵p1、p2是方程x2+ax+b=0的两个根,
∴p1+p2=-a,p1•p2=b
即a=-
| 3 |
| 4 |
| 9 |
| 64 |
点评:本题主要考查了古典概型的概率的求法和韦达定理的应用,属于基础题.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
下列函数中,最小值为6的是( )
A、y=x+
| ||
| B、y=ex+9•e-x | ||
C、y=sinx+
| ||
| D、y=log2x+9logx2 |
若a>0,b>0且4a2+b2=4,则a
的最大值是( )
| 1+b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
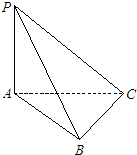 如图,已知PA⊥平面ABC,AB⊥BC,若PA=2,AB=1,BC=
如图,已知PA⊥平面ABC,AB⊥BC,若PA=2,AB=1,BC=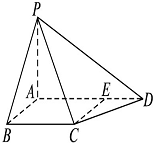 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,且CE∥AB.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,且CE∥AB.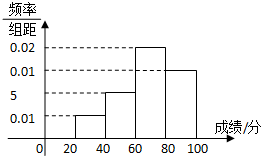 学校组织学生参加模块测试,测试后随机抽查部分学生的成绩,成绩的频率分布直方图如图5,数据的分组依次为[20,40),[40,60),[60,80),[80,100],低于60分的人数是6人
学校组织学生参加模块测试,测试后随机抽查部分学生的成绩,成绩的频率分布直方图如图5,数据的分组依次为[20,40),[40,60),[60,80),[80,100],低于60分的人数是6人