题目内容
已知sinα=
，cos（β-α）=
，且0＜α＜β＜
．
（1）求tan2α值；
（2）求cosβ值．
4
| ||
| 7 |
| 13 |
| 14 |
| π |
| 2 |
（1）求tan2α值；
（2）求cosβ值．
考点：两角和与差的余弦函数,两角和与差的正弦函数
专题：三角函数的求值
分析：（1）利用同角三角函数间的关系可求得tanα，由二倍角的正切公式即可求得tan2α值；
（2）利用同角三角函数间的关系及两角和与差的余弦函数即可求得cosβ的值．
（2）利用同角三角函数间的关系及两角和与差的余弦函数即可求得cosβ的值．
解答：
解：（1）∵sinα=
，0＜α＜
，
∴cosα=
=
，
∴tanα=4
，
∴tan2α=
=
=-
．
（2）∵cos（β-α）=
，且0＜α＜β＜
，
sin（β-α）=
=
，
∴cosβ=cos[（β-α）+α]=cos（β-α）cosα-sin（β-α）sinα=
×
-
×
=-
．
4
| ||
| 7 |
| π |
| 2 |
∴cosα=
| 1-sin2α |
| 1 |
| 7 |
∴tanα=4
| 3 |
∴tan2α=
| 2tanα |
| 1-tan2α |
8
| ||
| 1-48 |
8
| ||
| 47 |
（2）∵cos（β-α）=
| 13 |
| 14 |
| π |
| 2 |
sin（β-α）=
| 1-cos2(β-α) |
3
| ||
| 14 |
∴cosβ=cos[（β-α）+α]=cos（β-α）cosα-sin（β-α）sinα=
| 13 |
| 14 |
| 1 |
| 7 |
3
| ||
| 14 |
4
| ||
| 7 |
| 23 |
| 98 |
点评：本题考查同角三角函数间的关系与二倍角的正切、两角和与差的余弦函数的应用，考查转化思想与运算能力，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
若a＞0，b＞0且4a2+b2=4，则a
的最大值是（ ）
| 1+b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
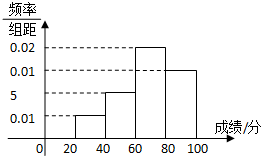学校组织学生参加模块测试，测试后随机抽查部分学生的成绩，成绩的频率分布直方图如图5，数据的分组依次为[20，40），[40，60），[60，80），[80，100]，低于60分的人数是6人