题目内容
在△ABC中,角A,B,C的对边分别为a,b,c,且(2a+c)cosB+bcosC=0
(1)求角B的大小.
(2)若b=
,a+c=4,求△ABC的面积.
(3)求y=sin2A+sin2C的取值范围.
(1)求角B的大小.
(2)若b=
| 13 |
(3)求y=sin2A+sin2C的取值范围.
考点:余弦定理的应用
专题:解三角形
分析:(1)利用正弦定理结合两角和的正弦公式,即可求角B的大小.
(2)利用余弦定理求出ac的值,即可求△ABC的面积.
(3)利用倍角公式,结合三角函数的图象和性质即可得到结论.
(2)利用余弦定理求出ac的值,即可求△ABC的面积.
(3)利用倍角公式,结合三角函数的图象和性质即可得到结论.
解答:
解:(1)∵(2a+c)cosB+bcosC=0,
∴(2sinA+sinC)cosB+sinBcosC=0
2sinAcosB+sin(B+C)=0,
即2sinAcosB+sinA=0,
∴cosB=-
,即B=
.
(2)若b=
,a+c=4,
则b2=a2+c2-2accosB=(a+c)2-2ac-2accosB,
即13=16-2ac+ac,
则ac=3,
∵a+c=4,
∴a=1c=3或a=3,c=1,
则△ABC的面积S=
acsinB=
×3×
=
.
(3)∵B=
,
∴A+C=
,即C=
-A,0<A<
,
则y=sin2A+sin2C=
+
=1-
[cos2A+cos(
-2A)]=1-
[
cos2A+
sin2A]=1-
sin(2A+
),
∵0<A<
,
∴
<2A+
<π,
则0<sin2A+
≤1,
则
≤1-
sin(2A+
)<1,
即y=sin2A+sin2C的取值范围是
≤y<1.
∴(2sinA+sinC)cosB+sinBcosC=0
2sinAcosB+sin(B+C)=0,
即2sinAcosB+sinA=0,
∴cosB=-
| 1 |
| 2 |
| 2π |
| 3 |
(2)若b=
| 13 |
则b2=a2+c2-2accosB=(a+c)2-2ac-2accosB,
即13=16-2ac+ac,
则ac=3,
∵a+c=4,
∴a=1c=3或a=3,c=1,
则△ABC的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
3
| ||
| 4 |
(3)∵B=
| 2π |
| 3 |
∴A+C=
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
则y=sin2A+sin2C=
| 1-cos2A |
| 2 |
| 1-cos2C |
| 2 |
| 1 |
| 2 |
| 2π |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 3 |
∵0<A<
| π |
| 3 |
∴
| π |
| 3 |
| π |
| 3 |
则0<sin2A+
| π |
| 3 |
则
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
即y=sin2A+sin2C的取值范围是
| 1 |
| 2 |
点评:本题主要考查正弦定理和余弦定理的应用,考查三角形的面积公式,涉及的公式较多.

练习册系列答案
相关题目
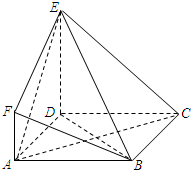 如图,四边形ABCD是边长为2的正方形,DE⊥平面ABCD,AF∥DE,DE=2AF,BE与平面ABCD所成角的正切值为
如图,四边形ABCD是边长为2的正方形,DE⊥平面ABCD,AF∥DE,DE=2AF,BE与平面ABCD所成角的正切值为