题目内容
已知f（a）=
（Ⅰ）化简f（a）；
（Ⅱ）若α是第三象限角，且cos（α-
π）=
，求f（a）的值；
（Ⅲ）求f（
）+f（
）+f（
）+…+f（
）的值．
| sin(π-α)cos(2π-α)tan(-α-π) |
| sin(-π-α) |
（Ⅰ）化简f（a）；
（Ⅱ）若α是第三象限角，且cos（α-
| 3 |
| 2 |
| 1 |
| 5 |
（Ⅲ）求f（
| π |
| 3 |
| 2π |
| 3 |
| 3π |
| 3 |
| 2013π |
| 3 |
考点：三角函数的化简求值,运用诱导公式化简求值
专题：三角函数的求值
分析：（Ⅰ）由条件利用诱导公式求得f（a）的值．
（Ⅱ）由α是第三象限角，且cos（α-
π）=
，利用同角三角函数的基本关系求得f（a）的值．
（Ⅲ）利用f（x）的周期性求得f（
）+f（
）+f（
）+…+f（
）的值．
（Ⅱ）由α是第三象限角，且cos（α-
| 3 |
| 2 |
| 1 |
| 5 |
（Ⅲ）利用f（x）的周期性求得f（
| π |
| 3 |
| 2π |
| 3 |
| 3π |
| 3 |
| 2013π |
| 3 |
解答：
解：（Ⅰ）利用诱导公式可得f(α)=
=sinα•cosα•
=-cosα．
（Ⅱ）∵
=cos(α-
)=-sinα，且α是第三象限的角∴cosα=-
=-
，
所以f(α)=
．
（Ⅲ）因为f(
)+f(
)+…+f(
)=0，且cos（2kπ+α）=cosα，
所以f(
)+f(
)+…+f(
)=f(
)+f(
)+f(
)=1．
sinα•cosα•
| ||||||||
| sin(-α-π) |
| -cosα |
| -sinα•(-cosα) |
（Ⅱ）∵
| 1 |
| 5 |
| 3π |
| 2 |
| 1-sin2α |
2
| ||
| 5 |
所以f(α)=
2
| ||
| 5 |
（Ⅲ）因为f(
| π |
| 3 |
| 2π |
| 3 |
| 6π |
| 3 |
所以f(
| π |
| 3 |
| 2π |
| 3 |
| 2013π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
| 3π |
| 3 |
点评：本题主要考查同角三角函数的基本关系、诱导公式的应用，以及三角函数在各个象限中的符号，利用函数的周期性奇函数的值，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
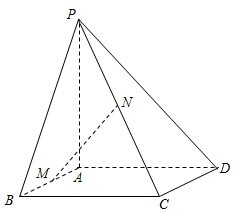如图，在四棱锥中，底面ABCD为矩形，PA⊥底面ABCD，M、N分别是AB、PC中点．