题目内容
若点P是曲线y=x2-lnx任意一点,则点P到直线y=x-2的最小值为 .
考点:利用导数研究曲线上某点切线方程
专题:计算题,作图题,导数的综合应用
分析:由题意作图,故当点P是曲线的切线中与直线y=x-2平行的直线的切点时,最近;从而解得.
解答:
解:由题意作图如下,

当点P是曲线的切线中与直线y=x-2平行的直线的切点时,最近;
故令y′=2x-
=1解得,x=1;
故点P的坐标为(1,1);
故点P到直线y=x-2的最小值为
=
;
故答案为:
.

当点P是曲线的切线中与直线y=x-2平行的直线的切点时,最近;
故令y′=2x-
| 1 |
| x |
故点P的坐标为(1,1);
故点P到直线y=x-2的最小值为
| |1-2-1| | ||
|
| 2 |
故答案为:
| 2 |
点评:本题考查了几何意义的运用及导数的综合应用,属于中档题.

练习册系列答案
相关题目
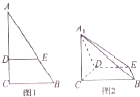 如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到A1DE的位置,使A2C⊥CD,如图2.
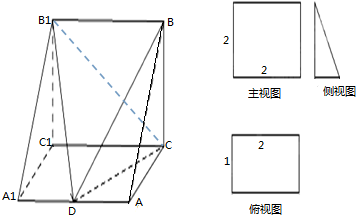
如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到A1DE的位置,使A2C⊥CD,如图2. 如图,在正四棱柱ABCD-A1B1C1D1中,E、F、G、H分别是CC1、C1D1、D1D、DC的中点,N是BC的中点,点M在四边形EFGH上或其内部运动,且使MN⊥AC.对于下列命题:
如图,在正四棱柱ABCD-A1B1C1D1中,E、F、G、H分别是CC1、C1D1、D1D、DC的中点,N是BC的中点,点M在四边形EFGH上或其内部运动,且使MN⊥AC.对于下列命题: