题目内容
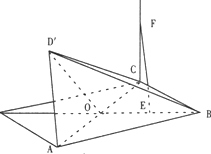 在菱形ABCD中,AC=2,BD=4,AC与BD交于0,将△ABC)沿着AC折起,使D点至点D′,且D′点到平面ABC距离为
在菱形ABCD中,AC=2,BD=4,AC与BD交于0,将△ABC)沿着AC折起,使D点至点D′,且D′点到平面ABC距离为| 3 |
(1)求证AC丄BD;
(2)E是BO的中点,过C作平面ABC的垂线l,直线l上是否存在一点F,使EF∥平面AD′C?若存在,求出CF的长;若不存在,请说明理由.
考点:直线与平面平行的性质,空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:(1)根据线面垂直的性质定理证明AC⊥平面BOD′即可证明AC丄BD;
(2)根据线面平行的判定定理进行判断即可.
(2)根据线面平行的判定定理进行判断即可.
解答:
 解:(1)设AC∩BD=0,
解:(1)设AC∩BD=0,
则菱形ABCD,AC⊥BD,
∴AC⊥OD′,AC⊥OB,
∵OD′∩OB=O,OD′?平面BOD′,OB?面BOD′,
∴AC⊥平面BOD′,
∴AC丄BD;
(2)过D′作D'H⊥DO,于H,连接CH,AH,AE,CE,
由(1)得平面BOD'⊥平面ABC,
故HD'⊥平面ABC,
故D'H=
,
∴OH=
=1=OE,
∴四边形AECH为平行四边形,
∴CH∥AE,CH=AE,
∴CH∥AE,CH=AE,
在l上截取CF=
,
∵HD'⊥平面ABC,CF⊥平面ABC,
∴CF∥DH,
又CF=DH=
,
∴四边形CFD'H为平行四边形,
∴CH∥D'F,CH=D'F,而CH∥AE,CH=AE,
∴AE∥D'F,D'F=AE,
∴四边形D'AEF为平行四边形,
∴AD'∥EF,
∵EF?平面AD'C,AD'?平面ADC,
∴EF∥平面AD'C,
故存在F,使EF∥平面AD′C,此时CF=
.
 解:(1)设AC∩BD=0,
解:(1)设AC∩BD=0,则菱形ABCD,AC⊥BD,
∴AC⊥OD′,AC⊥OB,
∵OD′∩OB=O,OD′?平面BOD′,OB?面BOD′,
∴AC⊥平面BOD′,
∴AC丄BD;
(2)过D′作D'H⊥DO,于H,连接CH,AH,AE,CE,
由(1)得平面BOD'⊥平面ABC,
故HD'⊥平面ABC,
故D'H=
| 3 |
∴OH=
| OD′2-D′H2 |
∴四边形AECH为平行四边形,
∴CH∥AE,CH=AE,
∴CH∥AE,CH=AE,
在l上截取CF=
| 3 |
∵HD'⊥平面ABC,CF⊥平面ABC,
∴CF∥DH,
又CF=DH=
| 3 |
∴四边形CFD'H为平行四边形,
∴CH∥D'F,CH=D'F,而CH∥AE,CH=AE,
∴AE∥D'F,D'F=AE,
∴四边形D'AEF为平行四边形,
∴AD'∥EF,
∵EF?平面AD'C,AD'?平面ADC,
∴EF∥平面AD'C,
故存在F,使EF∥平面AD′C,此时CF=
| 3 |
点评:本题主要考查空间直线和平面垂直和平行的判定,要求熟练掌握相应的判定定理,考查学生的推理能力.

练习册系列答案
相关题目
下列命题中是假命题的是( )
| A、?a,b∈R+,1g(a+b)≠1ga+1gb |
| B、?φ∈R,使得函数f(x)=sin(2x+φ)是偶函数 |
| C、?α,β∈R,使得sin(α+β)=sinα+sinβ |
| D、?m∈R,使f(x)=(m-1)•x m2-4m+3是幂函数,且在(0,+∞)上递减 |
设P是双曲线
-
=1(a>0)右支上一点,其一条渐近线方程是3x-2y=0,F1、F2分别是双曲线的左、右焦点,若|PF1|=8,则|PF2|等于( )
| x2 |
| a2 |
| y2 |
| 9 |
| A、4 | B、12 |
| C、4或12 | D、2或14 |
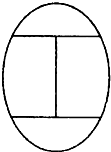 某校园有一椭圆型花坛,分成如图四块种花,现有4种不同颜色的花可供选择,要求每块地只能种一种颜色,且有公共边界的两块不能种同一种颜色,则不同的种植方法共有( )
某校园有一椭圆型花坛,分成如图四块种花,现有4种不同颜色的花可供选择,要求每块地只能种一种颜色,且有公共边界的两块不能种同一种颜色,则不同的种植方法共有( )| A、48种 | B、36种 |
| C、30种 | D、24种 |