题目内容
下列命题中是假命题的是( )
| A、?a,b∈R+,1g(a+b)≠1ga+1gb |
| B、?φ∈R,使得函数f(x)=sin(2x+φ)是偶函数 |
| C、?α,β∈R,使得sin(α+β)=sinα+sinβ |
| D、?m∈R,使f(x)=(m-1)•x m2-4m+3是幂函数,且在(0,+∞)上递减 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:利用举特例的方法说明四个选项中A错误,B,C,D正确.
解答:
解:对于A,∵当a=b=2时,有1g(a+b)=1ga+1gb,∴A为假命题;
对于B,当φ=
时,f(x)=sin(2x+
)=cos2x是偶函数,∴B为真命题;
对于C,当α=β=0时,sin(α+β)=sinα+sinβ,∴C为真命题;
对于D,当m=2时,f(x)=(m-1)•x m2-4m+3=x-1是幂函数,且在(0,+∞)上递减,D为真命题.
∴选项A是假命题.
故选:A.
对于B,当φ=
| π |
| 2 |
| π |
| 2 |
对于C,当α=β=0时,sin(α+β)=sinα+sinβ,∴C为真命题;
对于D,当m=2时,f(x)=(m-1)•x m2-4m+3=x-1是幂函数,且在(0,+∞)上递减,D为真命题.
∴选项A是假命题.
故选:A.
点评:本题考查了命题的真假判断与应用,考查了基本初等函数的性质,是基础题.

练习册系列答案
相关题目
阅读如图所示的程序框图,运行相应的程序,输出的结果是( )


| A、20 | B、21 |
| C、200 | D、210 |
某设计运动员在一次测试中射击10次,其测试成绩如表:则该运动员测试成绩的中位数为( )
| 环数 | 7 | 8 | 9 | 10 |
| 频数 | 3 | 2 | 2 | 3 |
| A、2 | B、8 | C、8.5 | D、9 |
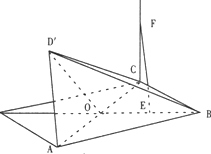 在菱形ABCD中,AC=2,BD=4,AC与BD交于0,将△ABC)沿着AC折起,使D点至点D′,且D′点到平面ABC距离为
在菱形ABCD中,AC=2,BD=4,AC与BD交于0,将△ABC)沿着AC折起,使D点至点D′,且D′点到平面ABC距离为