题目内容
设a1,a2,a3∈R+,且a1+a2+a3=m.求证:
(1)a12+a22+a32≥
;
(2)
+
+
≥
.
(1)a12+a22+a32≥
| m2 |
| 3 |
(2)
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 9 |
| m |
考点:不等式的证明
专题:证明题,不等式的解法及应用
分析:(1)(a1+a2+a3)2=a12+a22+a32+2a1a2+2a2a3+2a1a3≤3(a12+a22+a32),即可得出结论;
(2)根据基本不等式的性质可分别求得a1+a2+a3和
+
+
的最小值,两式相乘即可求得(
+
+
)m的最小值,整理后原式得证.
(2)根据基本不等式的性质可分别求得a1+a2+a3和
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
解答:
证明:(1)(a1+a2+a3)2=a12+a22+a32+2a1a2+2a2a3+2a1a3≤3(a12+a22+a32),
∵a1+a2+a3=m,
∴a12+a22+a32≥
;
(2)∵(
+
+
)m=(
+
+
)(a1+a2+a3)≥3
•3
,
当且仅当a1=a2=a3=
时等号成立.
又∵m=a1+a2+a3>0,
∴
+
+
≥
.
∵a1+a2+a3=m,
∴a12+a22+a32≥
| m2 |
| 3 |
(2)∵(
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 3 | a1a2a3 |
| 3 |
| ||||||
当且仅当a1=a2=a3=
| m |
| 3 |
又∵m=a1+a2+a3>0,
∴
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 9 |
| m |
点评:本题主要考查了基本不等式的应用.解题的时候要特别注意等号成立的条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
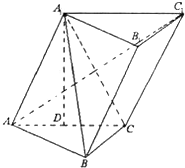 如图,斜三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=2,BA1⊥AC1,点A1在底面ABC上的射影恰为AC的中点D.
如图,斜三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=2,BA1⊥AC1,点A1在底面ABC上的射影恰为AC的中点D. 图中的三个直角三角形是一个几何体的三视图,
图中的三个直角三角形是一个几何体的三视图,