题目内容
要得到函数y=f′（x）的图象，需将函数f（x）=sinx-cosx（x∈R）的图象（ ）
A、向左平移
| ||
B、向右平移
| ||
| C、向左平移π个单位 | ||
| D、向右平移π个单位 |
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：利用两角和差的正弦公式化简f（x）、f′（x）的解析式，再根据函数y=Asin（ωx+φ）的图象变换规律，得出结论．
解答：
解：∵函数f（x）=sinx-cosx=
sin（x-
），∴f′（x）=cosx+sinx=
sin（x+
），
将函数f（x）=sinx-cosx=
sin（x-
）的图象向左平移
个单位，
可得函数y=f′（x）的图象，
故选：A．
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
将函数f（x）=sinx-cosx=
| 2 |
| π |
| 4 |
| π |
| 2 |
可得函数y=f′（x）的图象，
故选：A．
点评：本题主要考查函数y=Asin（ωx+φ）的图象变换规律，两角和差的正弦公式，属于基础题．
练习册系列答案
相关题目
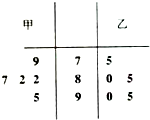甲、乙两位同学参加数学竞赛培训，在培训期间，他们参加的5次预赛成绩数据茎叶图如图，下列对提供的数据分析正确的是（ ）A、
| ||||
B、
| ||||
| C、S甲2＞S乙2 | ||||
| D、S甲2＜S乙2 |
若-
＜α＜0，则直线y=-xtanα+1的倾斜角为（ ）
| π |
| 2 |
| A、-α | ||
B、
| ||
| C、π+α | ||
D、
|
已知f（x）=x3-3x2+m，在区间[1，3]上任取三个数a，b，c，均存在以f（a），f（b），f（c）为边长的三角形，则m的取值范围是（ ）
| A、m＞2 | B、m＞4 |
| C、m＞6 | D、m＞8 |
二项式（x+2）11展开式中，二项式系数最大的项是（ ）
| A、第5项 | B、第5、6项 |
| C、第6项 | D、第6、7项 |
在空间直角坐标系中，点P在x轴正半轴上，它到Q（0，
，3）的距离为2
，则点P的坐标为（ ）
| 2 |
| 3 |
| A、（2，0，0） |
| B、（-1，0，0） |
| C、（0，0，1） |
| D、（1，0，0） |
“x＜2”是“x2＜4”的（ ）
| A、必要不充分条件 |
| B、充要条件 |
| C、充分不必要条件 |
| D、既不充分又非必要条件 |
已知函数f（x）=xlnx，则其在点（e，f（e））处的切线方程是（ ）
| A、y=2x-e | B、y=e |
| C、y=x-e | D、y=x+e |