题目内容
某工厂用A,B,C三种原料生产甲、乙两种产品,现有A,B,C三种原料分别为8吨、10吨、11吨;每生产一吨甲产品需要1吨A原料、2吨B原料、1吨C原料,可获利3万元;每生产一吨乙产品需要2吨A原料、1吨B原料、3吨C原料,可获利2万元;则该工厂最大可获利 万元.
考点:简单线性规划的应用
专题:应用题,不等式的解法及应用
分析:列出约束条件,再根据约束条件画出可行域,再利用利润z=3x+2y的几何意义求最值即可.
解答:
 解:设生产甲x吨,乙y吨,则
解:设生产甲x吨,乙y吨,则
(x,y∈N),
利润z=3x+2y,
可行域如图所示,由
,可得x=3.8,y=2.4,
结合图形可得x=4,y=2时,z=12+4=16.
故答案为:16.
 解:设生产甲x吨,乙y吨,则
解:设生产甲x吨,乙y吨,则
|
利润z=3x+2y,
可行域如图所示,由
|
结合图形可得x=4,y=2时,z=12+4=16.
故答案为:16.
点评:本题考查了列一元一次不等式组解实际问题的运用及一元一次不等式组的解法的运用,解答时找到题意中的不相等关系是建立不等式组的关键.

练习册系列答案
相关题目
下列所示的图形中,可以作为函数y=f(x)的图象的是( )
A、 |
B、 |
C、 |
D、 |
阅读如图所示程序:

若输出y=9,则输入的x值应该是( )

若输出y=9,则输入的x值应该是( )
| A、-1 | B、4或-1 |
| C、4 | D、2或-2 |
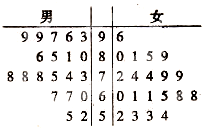 在某次数学考试中,从高一年级300名男生和300名女生中,各随机抽取20名学生的成绩进行统计,作出茎叶图如图所示:
在某次数学考试中,从高一年级300名男生和300名女生中,各随机抽取20名学生的成绩进行统计,作出茎叶图如图所示: